Chapter 14 Trigonometric Ratios of Acute Angles Ex 14.2

Rajasthan Board RBSE Class 9 Maths Solutions Chapter 14 Trigonometric Ratios of Acute Angles Ex 14.2

Solve the following by using trigonometric identities (1 to 10)
Question 1.
If cosec A = , then evaluate cot A, sin A and cos A.
Solution.

Question 2.
If tan A = , then evaluate cos A and sin A.
Solution.

Question 3.
If sin A =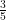 , then evaluate cos A and tan A.
Solution.

Question 4.
If cos B =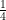 , then find the remaining trigonometrical ratios.
Solution.

Question 5.
If sin A = , then evaluate cos A and tan A.
Solution.

Question 6.
If tan A = √2 – 1, then prove that sin A cos A = 
Solution.

Question 7.
If tan A = 2, then evaluate sec A . sin A + tan2A – cosec A.
Solution.
tan A = 2 (given)

Question 8.
If sin θ =  then evaluate 
Solution.

Question 9.
If cos θ =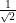 , then evaluate sin θ and cot θ
Solution.

Question 10.
If sec θ = 2, then evaluate tan θ, cos θ and sin θ.
Solution.
sec θ = 2 (given)
We know that 1 + tan2θ = sec2θ
tan2θ = sec2θ – 1