Rajasthan Board RBSE Class 9 Maths Solutions Chapter 14 Trigonometric Ratios of Acute Angles Ex 14.3
Question 1.
Prove that cos θ tan θ = sin θ.
Solution.
L.H.S. = cos θ tan θ
= cos θ x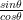
= sin θ
= R.H.S.
Hence proved.
Prove that cos θ tan θ = sin θ.
Solution.
L.H.S. = cos θ tan θ
= cos θ x
= sin θ
= R.H.S.
Hence proved.
Question 2.
Prove that (1 – sin2θ) tan2θ = sin2θ.
Solution.

Prove that (1 – sin2θ) tan2θ = sin2θ.
Solution.

Question 3.
Prove that
Solution.

Prove that
Solution.

Question 4.
Prove that
(sin θ + cos θ)2 + (sin θ – cos θ)2 = 2.
Solution.

Prove that
(sin θ + cos θ)2 + (sin θ – cos θ)2 = 2.
Solution.

Question 5.
Prove that
cosec6θ – cot6θ = 1 + 3 cosec2θ cot2θ.
Solution.

Prove that
cosec6θ – cot6θ = 1 + 3 cosec2θ cot2θ.
Solution.

Question 6.
Prove that
sin2θ cos θ + tan θ sin θ + cos3θ = sec θ.
Solution.

Prove that
sin2θ cos θ + tan θ sin θ + cos3θ = sec θ.
Solution.

Question 7.
Prove that
Solution.


Prove that
Solution.


Question 8.
Prove that

Solution.

Prove that

Solution.

Question 9.
Prove that

Solution.


Prove that

Solution.


Question 10.
Prove that

Solution.

Prove that

Solution.

Question 11.
Prove that

Solution.

Prove that

Solution.

Question 12.
Prove that

Solution.

Prove that

Solution.

Question 13.
Prove that

Solution.


Prove that

Solution.


Question 14.
Prove that (1 + cot θ – cosec θ)(1 + tan θ + sec θ) = 2
Solution.

Prove that (1 + cot θ – cosec θ)(1 + tan θ + sec θ) = 2
Solution.







0 Comments