Rajasthan Board RBSE Class 9 Maths Solutions Chapter 14 Trigonometric Ratios of Acute Angles Miscellaneous Exercise
Multiple Choice Questions
Question 1.
If tan θ = √3, then the value of sinθ is:
(A)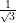
(B)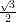
(C)
(D) 1
If tan θ = √3, then the value of sinθ is:
(A)
(B)
(C)
(D) 1
Question 2.
If sin θ = , then the value of tan θ is:
, then the value of tan θ is:
(A)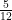
(B)
(C)
(D)
If sin θ =
(A)
(B)
(C)
(D)
Question 3.
If √3 cos A = sin A, then the value of cot A is:
(A) √3
(B) 1
(C)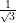
(D) 2
If √3 cos A = sin A, then the value of cot A is:
(A) √3
(B) 1
(C)
(D) 2
Question 4.
In figure, the value of cot A is:

(A)
(B)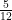
(C)
(D)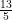
In figure, the value of cot A is:

(A)
(B)
(C)
(D)
Question 5.
In figure, the value of tan θ is:

(A) 2
(B)
(C)
(D)
In figure, the value of tan θ is:

(A) 2
(B)
(C)
(D)
Question 6.
In figure, the value of cosec α is:

(A)
(B)
(C)
(D)
In figure, the value of cosec α is:

(A)
(B)
(C)
(D)
Question 7.
The value of sin230° + cos230° is:
(A) 0
(B) 2
(C) 3
(D) 1
The value of sin230° + cos230° is:
(A) 0
(B) 2
(C) 3
(D) 1
Question 8.
The value of cosec255° – cot255° is:
(A) 1
(B) 2
(C) 3
(D) 0
The value of cosec255° – cot255° is:
(A) 1
(B) 2
(C) 3
(D) 0
Question 9.
If cot φ = then the value of cosec φ is:
then the value of cosec φ is:
(A)
(B)
(C)
(D)
If cot φ =
(A)
(B)
(C)
(D)
Question 10.
If in ∆ABC, ∠B = 90°, c = 12 cm and a = 9 cm then the value of cos C is:
(A)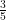
(B)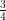
(C)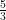
(D)
If in ∆ABC, ∠B = 90°, c = 12 cm and a = 9 cm then the value of cos C is:
(A)
(B)
(C)
(D)
Question 11.
The value of: (sec 40° + tan 40°)(sec 40° – tan 40°) is equal to:
(A) – 1
(B) 1
(C) cos 40°
(D) sin 40°
The value of: (sec 40° + tan 40°)(sec 40° – tan 40°) is equal to:
(A) – 1
(B) 1
(C) cos 40°
(D) sin 40°
Question 12.


Question 13.


Question 14.


Answers
1. B
2. A
3. C
4. B
5. D
6. B
7. D
8. A
9. C
10. A
11. B
12. A
13. C
14. D
1. B
2. A
3. C
4. B
5. D
6. B
7. D
8. A
9. C
10. A
11. B
12. A
13. C
14. D
Question 15.
If cosec θ = , then find the value of tan θ and cos θ.
, then find the value of tan θ and cos θ.
Solution.


If cosec θ =
Solution.


Question 16.
In an ∆ABC, if ∠B = 90° and AB = 12 cm and BC = 5 cm, then find the value of sin A, tan A, sin C and cot C.
Solution.
∆ABC is a right angled triangle right angled at B.


In an ∆ABC, if ∠B = 90° and AB = 12 cm and BC = 5 cm, then find the value of sin A, tan A, sin C and cot C.
Solution.
∆ABC is a right angled triangle right angled at B.


Question 17.

Solution.



Solution.


Question 18.

Solution.




Solution.



Question 19.
If cot A = √3, then prove that sin A cos B + cos A sin B = 1.
Solution.


If cot A = √3, then prove that sin A cos B + cos A sin B = 1.
Solution.


Question 20.

Solution.


Solution.

Question 21.

Solution.


Solution.

Question 22.

Solution.



Solution.


Question 23.

Solution.



Solution.


Question 24.
If sin A =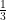 , then evaluate cos A . cosec A + tan A . sec A.
, then evaluate cos A . cosec A + tan A . sec A.
Solution.

If sin A =
Solution.

Question 25.

Solution.


Solution.

Question 26.

Solution.


Solution.

Question 27.

Solution.


Solution.

Question 28.

Solution.



Solution.


Question 29.

Solution.


Solution.

Question 30.
Prove that cos4θ – sin4θ = 1 – 2 sin2θ.
Solution.
L.H.S. = cos4θ – sin4θ
= (cos2θ)2 – (sin2θ)2
= (cos2θ – sin2θ)(cos2θ + sin2θ)
= (cos2θ – sin2θ) (1)
= (1 – sin2θ – sin2θ)
= 1 – 2 sin2θ
= R.H.S.
Hence proved.
Prove that cos4θ – sin4θ = 1 – 2 sin2θ.
Solution.
L.H.S. = cos4θ – sin4θ
= (cos2θ)2 – (sin2θ)2
= (cos2θ – sin2θ)(cos2θ + sin2θ)
= (cos2θ – sin2θ) (1)
= (1 – sin2θ – sin2θ)
= 1 – 2 sin2θ
= R.H.S.
Hence proved.
Question 31.
Prove that sec2θ – cosec2θ = tan2θ – cot2θ.
Solution.
L.H.S. = sec2θ – cosec2θ
= 1 + tan2θ – (1 + cot2θ)
= 1 + tan2θ – 1 – cot2θ
= tan2θ – cot2θ
= R.H.S.
Hence proved.
Prove that sec2θ – cosec2θ = tan2θ – cot2θ.
Solution.
L.H.S. = sec2θ – cosec2θ
= 1 + tan2θ – (1 + cot2θ)
= 1 + tan2θ – 1 – cot2θ
= tan2θ – cot2θ
= R.H.S.
Hence proved.
Question 32.

Solution.


Solution.

Question 33.
Prove that
(sin A + cosec A)2 + (cos A + sec A)2 = tan2A + cot2A + 7.
Solution.
L.H.S.
= (sin A + cosec A)2 + (cos A + sec A)2
= sin2A + cosec2A + 2 sin A cosec A + cos2A + sec2A + 2 cos A sec A

Prove that
(sin A + cosec A)2 + (cos A + sec A)2 = tan2A + cot2A + 7.
Solution.
L.H.S.
= (sin A + cosec A)2 + (cos A + sec A)2
= sin2A + cosec2A + 2 sin A cosec A + cos2A + sec2A + 2 cos A sec A

Question 34.

Solution.


Solution.







0 Comments