Rajasthan Board RBSE Class 9 Maths Solutions Chapter 14 Trigonometric Ratios of Acute Angles Ex 14.1
Question 1.
If in a triangle ABC, ∠A = 90°, a = 25 cm, b = 7 cm, then find all the trigonometrical ratios of ∠B and ∠C.
Solution.
Here it is given that
∠A = 90°, BC = 25 cm and AC = 7 cm
AB2 + AC2 = BC2
⇒ AB2 = BC2 – AC2


If in a triangle ABC, ∠A = 90°, a = 25 cm, b = 7 cm, then find all the trigonometrical ratios of ∠B and ∠C.
Solution.
Here it is given that
∠A = 90°, BC = 25 cm and AC = 7 cm
AB2 + AC2 = BC2
⇒ AB2 = BC2 – AC2


Question 2.
If in ∆ABC, ∠B = 90°, a = 12 cm, b = 13 cm, then find the trigonometrical ratios of ∠A and ∠C.
Solution.
Given that ∠B = 90°, AC = 13 cm, BC = 12 cm

If in ∆ABC, ∠B = 90°, a = 12 cm, b = 13 cm, then find the trigonometrical ratios of ∠A and ∠C.
Solution.
Given that ∠B = 90°, AC = 13 cm, BC = 12 cm

Question 3.
If tan A = √2 – 1 then prove that sin A cos A =
Solution.
tan A =
Now construct a triangle ABC in which
∠B = 90° and BC : AB = (√2 – 1) : 1
⇒ BC = (√2 – 1 )k, AB = k, where k is any constant


If tan A = √2 – 1 then prove that sin A cos A =
Solution.
tan A =
Now construct a triangle ABC in which
∠B = 90° and BC : AB = (√2 – 1) : 1
⇒ BC = (√2 – 1 )k, AB = k, where k is any constant


Question 4.
If sin A =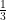 then find the value of cos A . cosec A + tan A . sec A
then find the value of cos A . cosec A + tan A . sec A
Solution.
sin A =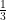
Now we will construct a triangle ABC in which ∠B = 90° and BC : AC = 1 : 3
Let BC = k and AC = 3k where k > 0 which is a constant quantity.

If sin A =
Solution.
sin A =
Now we will construct a triangle ABC in which ∠B = 90° and BC : AC = 1 : 3
Let BC = k and AC = 3k where k > 0 which is a constant quantity.

Question 5.
If cos θ = , then find all the remaining trigonometrical ratios.
, then find all the remaining trigonometrical ratios.
Solution.


If cos θ =
Solution.


Question 6.
If cos A = , then find the value of
, then find the value of 
Solution.


If cos A =
Solution.


Question 7.
If 5 tan θ = 4, then find the value of
Solution.


If 5 tan θ = 4, then find the value of
Solution.


Question 8.
In a ∆ABC, ∠C = 90° and if cot A = √3 and cot B =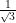 then prove that sin A cos B + cos A sin B = 1.
then prove that sin A cos B + cos A sin B = 1.
Solution.


In a ∆ABC, ∠C = 90° and if cot A = √3 and cot B =
Solution.


Question 9.
If 16 cot A = 12, then find the value of
Solution.

If 16 cot A = 12, then find the value of
Solution.

Question 10.
In figure, AD = DB and ∠B = 90° then find the value of the following:
(i) sin θ
(ii) cos θ
(iii) tan θ
Solution.
Given that AD = DB and ∠B = 90°


In figure, AD = DB and ∠B = 90° then find the value of the following:
(i) sin θ
(ii) cos θ
(iii) tan θ
Solution.
Given that AD = DB and ∠B = 90°








0 Comments