Rajasthan Board RBSE Class 9 Maths Solutions Chapter 13 Angles and their Measurement Miscellaneous Exercise
Multiple Choice Questions (Q1 to Q5)
Question 1.
The line describing an angle of 750°, lies in:
(A) First quadrant
(B) Second quadrant
(C) Third quadrant
(D) Fourth quadrant
Solution.
(A) First quadrant
The line describing an angle of 750°, lies in:
(A) First quadrant
(B) Second quadrant
(C) Third quadrant
(D) Fourth quadrant
Solution.
(A) First quadrant
Question 2.
The number of radians in angle 30° is:
(A) radian
radian
(B) radian
radian
(C) radian
radian
(D) radian
radian
Solution.
(C) radian
radian
The number of radians in angle 30° is:
(A)
(B)
(C)
(D)
Solution.
(C)
Question 3.
The value of in sexagesimal system is:
in sexagesimal system is:
(A) 75°
(B) 135°
(C) 120°
(D) 220°
Solution.
(B) 135°
The value of
(A) 75°
(B) 135°
(C) 120°
(D) 220°
Solution.
(B) 135°
Question 4.
The time is taken by the minute hand of a watch in tracing an angle of radians is:
radians is:
(A) 10 minutes
(B) 20 minutes
(C) 15 minutes
(D) 5 minutes
Solution.
(D) 5 minutes
The time is taken by the minute hand of a watch in tracing an angle of
(A) 10 minutes
(B) 20 minutes
(C) 15 minutes
(D) 5 minutes
Solution.
(D) 5 minutes
Question 5.
The value of the angle, in radian subtended at the centre of the circle of radius 100 metres by an arc of length 25π metres is:
(A) radian
radian
(B) radian
radian
(C) radian
radian
(D) radian
radian
Solution.
(A) radian
radian
The value of the angle, in radian subtended at the centre of the circle of radius 100 metres by an arc of length 25π metres is:
(A)
(B)
(C)
(D)
Solution.
(A)
Question 6.
In which quadrant does the revolving ray lie when it makes the following angles.
(i) 240°
(ii) 425°
(iii) -580°
(iv) 1280°
(v) -980°
Solution.
(i) 240° = 2 x right angle +60°, therefore the position of the revolving ray will be in third quadrant.
(ii) 425° = 4 x right angles +65°, therefore the position of the revolving ray will be in first quadrant.
(iii) -580° = – 6 x right angles -40°, therefore the position of the revolving ray will be in second quadrant.
(iv) 1280° = 14 x right angles +20°, therefore the position of the revolving ray will be in third quadrant.
(v) – 980° = – 10 x right angles -80°, therefore the position of the revolving ray will be in second quadrant.
In which quadrant does the revolving ray lie when it makes the following angles.
(i) 240°
(ii) 425°
(iii) -580°
(iv) 1280°
(v) -980°
Solution.
(i) 240° = 2 x right angle +60°, therefore the position of the revolving ray will be in third quadrant.
(ii) 425° = 4 x right angles +65°, therefore the position of the revolving ray will be in first quadrant.
(iii) -580° = – 6 x right angles -40°, therefore the position of the revolving ray will be in second quadrant.
(iv) 1280° = 14 x right angles +20°, therefore the position of the revolving ray will be in third quadrant.
(v) – 980° = – 10 x right angles -80°, therefore the position of the revolving ray will be in second quadrant.
Question 7.
Convert the following angles in radians:
(i) 45°
(ii) 120°
(iii) 135°
(iv) 540°
Solution.

Convert the following angles in radians:
(i) 45°
(ii) 120°
(iii) 135°
(iv) 540°
Solution.

Question 8.
Express the following angles in sexagesimal system.
(i)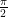
(ii)
(iii)
(iv)
Solution.

Express the following angles in sexagesimal system.
(i)
(ii)
(iii)
(iv)
Solution.

Question 9.
Find the angle in radians subtended at the centre of a circle of radius 5 cm by an arc of the circle whose length is 12 cm.
Solution.
We know that:
θ(radian) =
We have, radius = 5 cm and arc length = 12 cm
θc =
Find the angle in radians subtended at the centre of a circle of radius 5 cm by an arc of the circle whose length is 12 cm.
Solution.
We know that:
θ(radian) =
We have, radius = 5 cm and arc length = 12 cm
θc =
Question 10.
How much time the minute hand of a watch will take to describe an angle of radians.
radians.
Solution.
Time taken by the minute hand of a watch in tracing 4 right angles or an angle equal to 2π radians = 1 hour.
Time taken by the minute hand of a clock in tracing an angle equal to 1 radian = hours
hours
Time taken by the minute hand of a clock in tracing an angle equal to radians
radians

How much time the minute hand of a watch will take to describe an angle of
Solution.
Time taken by the minute hand of a watch in tracing 4 right angles or an angle equal to 2π radians = 1 hour.
Time taken by the minute hand of a clock in tracing an angle equal to 1 radian =
Time taken by the minute hand of a clock in tracing an angle equal to

Question 11.
How much time the minute hand of a watch will take to describe an angle of 120°?
Solution.
We know that:
The minute hand of a watch describes an angle of 4 right angles i.e. 360° in one hour.
the time taken by minute hand to trace 1° = hours
hours
the time taken by minute hand to trace 120° angle = x 120 =
x 120 = 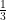 hours
hours
=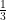 x 60 minutes = 20 minutes.
x 60 minutes = 20 minutes.
How much time the minute hand of a watch will take to describe an angle of 120°?
Solution.
We know that:
The minute hand of a watch describes an angle of 4 right angles i.e. 360° in one hour.
the time taken by minute hand to trace 1° =
the time taken by minute hand to trace 120° angle =
=
Question 12.
Find the radius of the circle, if any arc length of 10 cm subtends an angle of 60° at the centre of the circle.
Solution.

Find the radius of the circle, if any arc length of 10 cm subtends an angle of 60° at the centre of the circle.
Solution.

Question 13.
Find the time if the minute hand of a clock has revolved through 30 right angles just after noon.
Solution.
We know that:
The time taken by the minute hand of a clock in tracing 4 right angles is 1 hour.
So, we convert 30 right angles in terms of the multiple of 4 right angles
i.e. 30 right angles
= 7 x (4 right angles) + 2 right angles
= 7 x 1 hr + hr = 7
hr = 7 hours
hours
= 7 hours 30 minutes
Hence, time = 7 : 30 p.m.
Find the time if the minute hand of a clock has revolved through 30 right angles just after noon.
Solution.
We know that:
The time taken by the minute hand of a clock in tracing 4 right angles is 1 hour.
So, we convert 30 right angles in terms of the multiple of 4 right angles
i.e. 30 right angles
= 7 x (4 right angles) + 2 right angles
= 7 x 1 hr +
= 7 hours 30 minutes
Hence, time = 7 : 30 p.m.
Question 14.
The angles of a triangle are in the ratio of 2 : 3 : 4. Find all the three angles in radians.
Solution.
The A, B and C are angles of any triangle ABC
A : B : C = 2 : 3 : 4
⇒ ∠A = 2x, ∠B = 3x and ∠C = 4x
∠A + ∠B + ∠C = 180° (Angles sum property of a triangle)
⇒ 2x + 3x + 4x = 180°
⇒ 9x = 180°
x = 20°
Therefore angles (in degrees) are 40°, 60° and 80°


The angles of a triangle are in the ratio of 2 : 3 : 4. Find all the three angles in radians.
Solution.
The A, B and C are angles of any triangle ABC
A : B : C = 2 : 3 : 4
⇒ ∠A = 2x, ∠B = 3x and ∠C = 4x
∠A + ∠B + ∠C = 180° (Angles sum property of a triangle)
⇒ 2x + 3x + 4x = 180°
⇒ 9x = 180°
x = 20°
Therefore angles (in degrees) are 40°, 60° and 80°


Question 15.
Convert radian into sexagesimal system.
radian into sexagesimal system.
Solution.

Convert
Solution.







0 Comments