Chapter 4 Linear Equation and Inequalities in Two Variables Ex 4.1

RBSE Solutions for Class 10 Maths Chapter 4 Linear Equation and Inequalities in Two Variables Ex 4.1.

Class 10 Maths Chapter 4 Linear Equation and Inequalities in Two Variables Ex 4.1 solution. Solution is provided in this post. Here we have provide the solutions of RBSE Boards Books according to chapter wise.

Chapter 4 Linear Equation and Inequalities in Two Variables Ex 4.1

Question 1
By comparing  and  find,
whether the following pair of linear equations is consistent or inconsistent.
(i) 2r – 3y = 8; 4c – 6y = 9
(ii) 3x – y = 2; 6x – 2y = 4
(iii) 2x – 2y = 2; 4x – 4y = 5
(iv)  + 2y = 8; 2x + 3y = 12
Solution:
(i) Given linear pair of equations
23 – 3y = 8 or 2x – 3y – 8 = 0
and 4x – 6y = 9 or 4x – 6y – 9 = 0
Comparing above equations by a1 x + b1y + c1and a2 x + b2 y + c2 = 0,
a1 = 2, b1 = – 3, c1 = – 8
and a2 = 4, b2 = – 6, c2 = – 9.

∴ 
∴ Given linear pair has no solution.
So, given linear pair is inconsistent.

(ii) Given pair of linear equations
3x – y= 2
or 3x – y – 2 = 0 …(i)
and 6x – 2y = 4
or 6x – 2y – 4 = 0
or 3x – y – 2 = 0…(ii)
Comparing equations (i) and (ii) by a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0
a1 = 3, b1 = -1, and c1 = -2
and a2 = 3, b2 = -1 and c2= -2

Linear pair is coincident, so linear pair has infinite solutions.
Thus given pair is consistant.

(iii) Given linear pair
2x – 2y = 2
or 2x – 2y – 2 = 0
or x – y – 1 = 0 …(i)
and 4x – 4y – 5 = 0 …(ii)
Comparing equations (i) and (ii) by a1x + b1y+c1 = 0 and a2x + b2y + c2 = 0
a1 = 1, b1 = -1, and c1 = -1
and a2 = 4, b2 = -4 and c2= -5

Given linear pair has no solution.
Thus given Linear pair is inconsistent.

(iv) Given linear pair
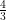x + 2y = 8
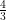x + 2y – 8 = 0 …(i)
and 2x + 3y = 12
2x + 3y – 12 = 0 …(ii)
Comparing equation (i) and (ii) by pair a1x + b1y+c1 = 0 and a2x + b2y + c2 = 0

Given linear pair has infinite solutions, so linear pair is consistent.

Chapter 4 Linear Equation and Inequalities in Two Variables Ex 4.1

Question 2
Solve the following pair of linear equations graphically and write nature of solution.
(i) x + y = 3; 3x – 2y = 4
(ii) 2x – y = 4; x + y = -1
(iii) x + y = 5; 2x + 2y = 10
(iv) 3x + y = 2; 2x – 3y = 5
Solution:
(i) Given linear pair
x + y = 3
x + y -3 = 0 ….(i)
3x – 2y = 4
3x – 2y – 4 = 0 ………(ii)
Comparing equation (i) and (ii) by pair a1x + b1y+c1 = 0 and a2x + b2y + c2 = 0
a1 = 1, b1 = 1, and c1 = -3
and a2 = 3, b2 = -2 and c2= -4

Linear pair has unique solution.
Thus, linear pair is consistent.

Graphical Method:
By equation (i),
x + y = 3
x = 3 – y
Putting y = 0, x = 3 – 0 =3
Putting y = 1, x = 3 – 1 = 2
Putting y = 2, x = 3 – 2 = 1
Table 1 for equation (i),

Table 2 for equation (ii),

Plot the points of Table (1) and (2) on graph paper and by joining these points, two straight lines are obtained.

From above graph, it is clear that two straight lines cut at point P(2, 1). Thus x = 2 and y = 1 is required solution.

(ii) Given linear pair
2x – y = 4
2x – y – 4 = 0 …..(i)
x + y = -1
x + y + 1 = 0 ….(ii)
Comparing equation (i) and (ii) by linear pair
a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0

Linear pair is consistent which will have unique solutions.

Graphical Method:
By equation (i),
2x – y = 4
Putting x = 0, 2 x 0 – y = 4
y = -4
Putting x = 1, 2 x – y = 4
-y = 4 – 2
Putting x = 2, 2 x 2 – y = 4
4 – y =4
y = 0

By equation (ii),
x + y = -1
Putting x = 0. 0 + y = -1
y = -1
Putting x = 1, +1 + y = -1
y = -1 – 1
y = -2
Putting x = 2,
2 + y = -1
y = -3

By plotting the points of Table 1 and 2 we get two straight lines.

From above graph, It is clear that both the straight lines cut each other at point P( 1, – 2).
Thus, x = 1,y = – 2 are required solution.

Chapter 4 Linear Equation and Inequalities in Two Variables Ex 4.1

(iii) Given linear pair:
x + y = 5 or x + y – 5 = 0 …(i)
2x + 2y = 10 or 2x + 2y – 10 = 0 ……..(ii)
Comparing above pair by general linear pair
a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0

∴ Lines represented linear pair will be coincident and linear pair will have infinite solutions.
Thus, given linear pair is consistent.

Graphical Method:
By equation (i),
x + y = 5
⇒ x = 5 – y
Putting y = 0, x = 5 – 0 = 5
Putting y = 3, x = 5 – 3 = 2
Putting y = 5, x =5 – 5 = 0

By joining the points A(5, 0), B(2, 3) and C(0, 5) on graph paper.
We get a straight line which indicates the equation x + y = 5.
By equation (ii),
2x + 2y = 10
⇒ 2(x + y) = 10
⇒ x + y =5
⇒ x = 5 – y
Putting y = 0, x = 5 – 0 = 5
Putting y = 2, x = 5 – 2 = 3
Putting y = 5, x = 5 – 5 = 0

By joining the points A(5, 0), 8(3,2) and C(0, 5) on graph paper we get a straight line which indicates the equation 2x + 2y = 10.

From graph, lis clear that given pair of linear equations are coincident. Thus they have infinitely many solutions.

(iv) Given pair of linear equations
3x + y = 2 or 3x + y – 2 = 0
2x – 3y = 5 or 2x – 3y – 5 = 0 …(ii)
Comparing equation (i) and (ii) by pair
a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0

Thus given equation will have unique solutions.
∴ Given pair is consistent.

Graphical Method:
By equation (i)
3x + y = 2
y = 2 – 3x
Putting x = 0, y = -3 x 0
y = 2
Putting x = -1, y = 2 – 3 x (-1)
y = 2 + 3
y = 5

From Table (1) arid (2), plot the points on graph paper and by joining them, we get two straight lines.

From above graph, It is clear that two straight lines intersect each other at point P( 1, – 1)
Thus, x = 1 and y = – 1 is required solution.

Question 3
Solve the following pair of linear equations, graphically and find the coordinates of that points where lines represented by these cuts y-axis.
(i) 2x – 5y + 4 = 0; 2x + y – 8 = 0
(ii) 3x + 2 = 12 ; 5x – 2y = 4
Solution:
(i) Given pair of linear equations
2x – 5y + 4 = 0 …(i)
and 2x + y – 8 = 0 …(ii)
From equation (i),

By equation (ii),
2x + y – 8 = 0
or y – 2x + 8 = 0
Putting x = 4, y = – 2 x 4 + 8
= -8 + 8
= 0
Putting x = 3, y = – 2 x 3 + 8
= -6 + 8
= 2
Putting x = 2, y = – 2 x 2 + 8
= -4 + 8
= 4

Plot the points from Table (1) and (2) on graph.
By joining these points two straight lines are obtained.

From above graph ¡t is clear that two straight lines intersect each other at point P(3, 2).
∴ Its required solutions are x = 3 and y = 2
and two straight lines cuts the y-axis at (0, 0.8) and (0, 8).

Chapter 4 Linear Equation and Inequalities in Two Variables Ex 4.1

(ii) Given pair of linear equations
3x + 2y = 12 …(i)
and 5x – 2y = 4 …(ii)
From equation (i),
3x + 2y = 12


Plot the points from Table (1) and (2) on graph paper. By joining these points two straight lines are obtained.

From above graph, it is clear that two straight lines intersect each other at point P(2, 3).
∴ x = 2 and y = 3 are required solutions and two straight lines cuts y-axis at (0, 6) and (0, – 2).

Question 4
Solve the following pair of linear equations grapycally and find the coordinates of the triangle so formed with the y-axis and the lines.
4x – 5y = 20,
3x + 5y = 15
Solution:
Given, pair of linear equation
4x – 5y = 20 ………..(i)
and 3x + 5y = 15 ………(ii)
From equation (i),
4x – 5y = 20
5y = 4x – 20


Plot the points obtained from Table (1) and (2) on graph paper. By joining these points two straight lines are obtained.

From the above graph it is clear that two lines intersect each other at point P(5, 0)
∴ x = 5 and y = 0 are required solution.
(0, 3), (0, – 4) and (5, 0) are co-ordinates of vertices of ΔABP formed by two straight lines at y – axis.

Chapter 4 Linear Equation and Inequalities in Two Variables Ex 4.1

Hope that the Solutions provided here for Class 10 Maths Chapter 4 Linear Equation and Inequalities in Two Variables Ex 4.1. will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 4 Linear Equation and Inequalities in Two Variables Ex 4.1 solution drop a comment below and like and share the post.

Thank you.