Chapter 2 Real Numbers Miscellaneous Exercise

RBSE Solutions for Class 10 Maths Chapter 2 Real Numbers Miscellaneous Exercise solution.

Class 10 Maths Chapter 2 Real Numbers Miscellaneous Exercise solution. Solution is provided in this post. Here we have provide the solutions of RBSE Boards Books according to chapter wise.

Chapter 2 Real Numbers Miscellaneous Exercise

RBSE Solutions for Class 10 Maths Chapter 2 Real Numbers Miscellaneous Exercise solution.

Question 1.
Sum of the power of prime factors of 196
(a) 1
(b) 2
(c) 4
(d) 6
Solution

196 = 22 x 72
Sum of powers =2 + 2 = 4
So, correct choice is (c).

Question 2.
If two numbers are written in the form m = pq3 and n = p3q2 then HCF of m, n whereas p, q prime numbers are:
(a) pq
(b) pq2
(c) p2q2
(d) p3q3
Solution

Chapter 2 Real Numbers Miscellaneous Exercise

Question 3.HCF of 95 and 152 is:

(a) 1
(b) 19
(c) 57
(d) 38
Solution
95 = 5 x 19
and 152 = 23 x 19
H.C.F. = 19
Hence, correct choice is (b).

Question 4.
Product of two is 1080 and their HCF is 30 then their LCM is:
(a) 5
(b) 16
(c) 36
(c) 108
Solution
Product of both numbers = H.C.F. x L.C.M.
1080 = 30 x L.C.M
L.C.M = 36
Hence, correct choice is (c)

Question 5.
Decimal expansion of number  will be:
(a) Terminating
(b) Non-terminating repeating
(c) Terminating and non-terminating both
(d) Non-rational
Solution
Since denominator is a factor the form of 2m x 5n
So correct choice is (a)

Question 6.
In the decimal expansion of rational number \frac { 43 }{ { 2 }^{ 2 }\times { 5 }^{ 3 } }, after how many digits decimal will end?
(a) 1
(b) 2
(c) 3
(d) 4
Solution

Chapter 2 Real Numbers Miscellaneous Exercise

Question 7.
The least number, which multiplies by √27 gives a natural number, will be :
(a) 3
(b) √3
(c) 9
(d) 3√3
Solution
√27 = 3√3
After multiple √3 use finds a natural number So, the correct choice is (b).

Question 8.
If HCF = LCM for two rational numbers, the numbers should be
(a) Composite
(b) Equal
(c) Prime
(d) Co-prime
Solution
The correct choice is (b)

Chapter 2 Real Numbers Miscellaneous Exercise

Question 9.
If LCM of a and 18 is 36 and HCF of a and 18 is 2 then value of a will be:
(a) 1
(b) 2
(c) 5
(d) 4
Solution
Since two numbers are and 18
H.C.F. = 2
L.C.M. = 36
Product of both = H.C.F. x L.C.M.
a x 18 = 2 x 36
a = 4
Hence, correct choice is (d).

Question 10.
If n is a natural number, then unit digit in 6n – 5n is:
(a) 1
(b) 6
(c) 5
(d) 9
Solution
The correct choice is (a).

Question 11.
If  (q ≠ 0) is a rational number then what condition apply for q whereas  is a terminating decimal ? Is a rational number is terminating decimal.
Solution
 (q ≠ 0) is a rational number.
and  is terminating decimal.
Prime factor of q will be in the form 2m x 5n where m, n is non-negative integers.

Question 12.
Simplify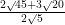  and clear whether it is rational or irrational number.
Solution


So, the given number is a rational number.

Question 13.
Prove that any positive odd integer is of the form 4q + 1 or 4q + 3, where q is any integer.
Solution
Let a is any positive odd integer and b = 4.
Applying Euclid division lemma in a, b
Where o ≤ r < 4 and q is any integer.
r = 0, 1, 2, 3 put
a = 4q + 0 ⇒ a = 4q
a = 4q + 1
a = 4q + 2
a = 4q + 4
For positive odd integer.
a ≠ 4 q, a ≠ 4q + 2
Hence, any odd integer is of the form 4q + 1, or 4q + 3.
Hence proved.

Chapter 2 Real Numbers Miscellaneous Exercise

Question 14.
Prove that the product of two consecutive positive integers is divisible by 2.
Solution
Let two consecutive positive integers is n, and (n + 1)
Product of both integers = n(n + 1) = n2 + n
We know that any positive integer is in the form 2q and 2q + 1. where q is an integer.
Here two cases are possible
Case. I. when n = 2q then
⇒ n2 + n = (2q)2 + (2q)
⇒ n2 + n = 4q2 + 2q
⇒ n2 + n = 2q(2q + 1) [Let r = q(2q + 1)]
⇒ n2 + n = 2r
⇒ n2 + n, 2 can be divided by 2
⇒ n(n + 1), also divided by 2
So, product of two consecutive positive integer is divided by 2
Hence proved.

Question 15.
Find the largest number which is divided by 2053 and 967, left the remainder as 5 and 7 respectively.
Solution
Given that on dividing 2053, there is a remainder of 5.
This means that 2053 – 5 = 2048 is exactly divisible by the required number.
Similarly, 967 – 7 = 960 is exactly divisible by the required number.

Question 16.
Explain, why 7 x 11 x 13 + 13 and 7 x 6 x 5 x 4 x 3 x 2 x 1 x 5 are composite numbers?
Solution
7 x 11 x 13 + 13 = 13[7 x 11 + 1]
= 13(77 + 1)
= 13 x 78
= 13 x 2 x 3 x 13
= 2 x 3 x 13 x 13
2, 3 and 13 are prime numbers.
So according to the fundamental theorem of arithmetic, every composite number can be uniquely expressed as a product of prime numbers.
So, this is a composite number
Similarly
7 x 6 x 5 x 4 x 3 x 2 x 1 + 5
= 5[7 x 6 x 4 x 3 x 2 x 1 + 1]
= 5(1008 + 1)
= 5 x 1009
5 and 1009 are prime numbers.
So according to the fundamental theorem of arithmetic is a composite number.

Chapter 2 Real Numbers Miscellaneous Exercise

Question 17.
If HCF of two numbers 306 and 657 is 9, then find their LCM.
Solution
We know that

Question 18.
A rectangular veranda is of dimension 18 m 72 cm x 13 m 30 cm. Squared tiles are used to cover them. Find the least number of such tiles.
Solution
length of varanda = 18 m 72 cm = (1800 + 72) cm = 1872 cm
and breadth = 13 m 20 cm = (1300 + 20) cm = 1320 cm
For finding the area of one tile we find the HCF of length and breadth.

Chapter 2 Real Numbers Miscellaneous Exercise

Question 19.
Prove that following numbers are irrational numbers
(i) 5√2
(ii) 
(iii) 
(iv) 4 + √2
Solution




a, b, ab and 4 all are integers.
 is a rational number.
√2 will be a rational number
This contradicts.
our hypothesis is wrong.
So, 4 + √2 is an irrational number.
Hence proved.

Question 20.What can you say about the prime factors of denominator of the following rational numbers.

(i) 34.12345
(ii) 
Solution
(i) 34.12345 = 
This number is in the form of 
This is a rational number.
q = 100000 = (10)5 = (2 x 5)5 = 25 x 55
So, prime factor of q are in the form of = 2 or 5.
(ii) 
= 43.123456789 123456789 123456789 …
The decimal expansion of this number is non-terminating and recurring and it is possible to write in the form .
This is a rational number.
So, besides 2 and 5 the prime factor of q, there are other prime positive integers possible.
Hence, the given number is rational.

Hope that the Solutions provided here for Class 10 Maths Chapter 2 Real Numbers Miscellaneous Exercise solution. will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 2 Real Numbers Miscellaneous Exercise solution drop a comment below and like and share the post.

Thank you.