Rajasthan Board RBSE Class 10 Maths Chapter 11 Similarity Ex 11.2
Question 1.
D and E are to points on the sides AB and AC of ΔABC, respectively. Such that DE || BC, then
(i) In AD = 6 cm, DB = 9 cm and AE = 8 cm then find AC.
(ii) If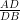 =
=  and AC = 20.4 cm. Then find EC.
and AC = 20.4 cm. Then find EC.
(iii)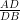 =
=  and AE = 6.3 cm then find AC.
and AE = 6.3 cm then find AC.
(iv) In AD = 4x – 3, AE = 8x – 7, BD = 3x – 1 and CE = 5x – 3 then find x.
Solution :
(i) In ∆ABC, DE || BC



D and E are to points on the sides AB and AC of ΔABC, respectively. Such that DE || BC, then
(i) In AD = 6 cm, DB = 9 cm and AE = 8 cm then find AC.
(ii) If
(iii)
(iv) In AD = 4x – 3, AE = 8x – 7, BD = 3x – 1 and CE = 5x – 3 then find x.
Solution :
(i) In ∆ABC, DE || BC



Question 2.
Points D and E lie on sides AB and AC of ΔABC, respectively. In the following questions check whether DE || BC or not.
(i) AB = 12 cm, AD = 8 cm, AE = 12 cm and AC = 18 cm
(ii) AB = 5.6 cm, AD = 1.4 cm, AC = 9.0 cm and AE = 1.8 cm
(iii) AD = 10.5 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm
(iv) AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and EC = 5.5 cm
Solution :


Points D and E lie on sides AB and AC of ΔABC, respectively. In the following questions check whether DE || BC or not.
(i) AB = 12 cm, AD = 8 cm, AE = 12 cm and AC = 18 cm
(ii) AB = 5.6 cm, AD = 1.4 cm, AC = 9.0 cm and AE = 1.8 cm
(iii) AD = 10.5 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm
(iv) AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and EC = 5.5 cm
Solution :


Question 3.In given figure, L, M and N are points on OA, OB and OC such that LM || AM and MN || BC then show that LN || AC.

Solution :
Given : In ∆ABC, point L,M, N respectively lie OA, OB and OC such that LM || AB and MN || BC.
To prove : LN || AC
Proof : In ∆ABO
LM || AB (given)
Again, In ∆BCO
MN || BC
From equation (i) and (ii),
⇒
⇒ LN || AC
Question 4.
In ∆ABC, D and E points lie on sides AB and AC such that BD = CE. If ∠B = ∠C then show that DE || BC.
Solution :
In ∆ABC, D and E lie on sides BD = CE and ∠B = ∠C
To prove : DE || BC

Proof : In ∆ABC,
∠B = ∠C
∴ AB = AC (opposite sides of equals angles are same)
⇒ AD + DB = AE + CE [∵ DB = CE given]
⇒ AD = AE
∵ ∠D = ∠E [Opposite angles of equal sides are same]
⇒ ∆ADE is an isosceles triangle
So, ∆ABC and ∆ADE are isosceles triangle in which vertex angle ∠A is common in both triangles.
∴ ∠B = ∠C = ∠D = ∠E
∠B = ∠D [corresponding angle]
⇒ DE || BC
In ∆ABC, D and E points lie on sides AB and AC such that BD = CE. If ∠B = ∠C then show that DE || BC.
Solution :
In ∆ABC, D and E lie on sides BD = CE and ∠B = ∠C
To prove : DE || BC

Proof : In ∆ABC,
∠B = ∠C
∴ AB = AC (opposite sides of equals angles are same)
⇒ AD + DB = AE + CE [∵ DB = CE given]
⇒ AD = AE
∵ ∠D = ∠E [Opposite angles of equal sides are same]
⇒ ∆ADE is an isosceles triangle
So, ∆ABC and ∆ADE are isosceles triangle in which vertex angle ∠A is common in both triangles.
∴ ∠B = ∠C = ∠D = ∠E
∠B = ∠D [corresponding angle]
⇒ DE || BC
Question 5.
In fig. DE || BC and CD || EF then prove that : AD2 = AB × AF

Solution :
Given : ∆ABC in which DE || BC and CD || EF
To prove : AD2 = AB × AF
Proof : In ∆ABC
DE || BC


In fig. DE || BC and CD || EF then prove that : AD2 = AB × AF

Solution :
Given : ∆ABC in which DE || BC and CD || EF
To prove : AD2 = AB × AF
Proof : In ∆ABC
DE || BC


Question 6.
In fig., EF || DC || AB Then prove that : =
= 

Solution :
Given : EF || DC || AB
To prove : =
= 

Construction : Join AC
Proof : In ∆ADC
GE || DC
∴ =
=  ….(i) (By Basic proportionality theorem)
….(i) (By Basic proportionality theorem)
Now In ∆ABC
AB || GF
∴ =
=  (By Basic Prop. Theorem)
(By Basic Prop. Theorem)
or =
=  ….(ii)
….(ii)
From equation (i) and (ii)
 =
= 
In fig., EF || DC || AB Then prove that :

Solution :
Given : EF || DC || AB
To prove :

Construction : Join AC
Proof : In ∆ADC
GE || DC
∴
Now In ∆ABC
AB || GF
∴
or
From equation (i) and (ii)
Question 7.
ABCD is a parallelogram. P is any point on side BC of ||gm. If DP and AB produced, meet at L then prove that:
(i) =
= 
(ii) =
= 
Solution :
Given : ABCD ¡s a parallelogram. Point P lies on side BC. Produced DP and AB meet at point L.
(i) To prove : =
= 

Proof : In ∆LDA
BP || AD
 =
=  (By B.P. Theorem)
(By B.P. Theorem)
or =
=  [∵ AB = CD sides of ||gm]
[∵ AB = CD sides of ||gm]
⇒ =
= 
(ii) To prove

ABCD is a parallelogram. P is any point on side BC of ||gm. If DP and AB produced, meet at L then prove that:
(i)
(ii)
Solution :
Given : ABCD ¡s a parallelogram. Point P lies on side BC. Produced DP and AB meet at point L.
(i) To prove :

Proof : In ∆LDA
BP || AD
or
⇒
(ii) To prove

Question 8.
Point D and E lie on side AB of ∆ABC such that AD = BE. If DP || BC and EQ || AC then prove that PQ || AB.
Solution :
Given : ∆ABC in which
AD = BE,
DP || BC and EQ || AC
To prove PQ || AB

Proof : In ∆ABC DP || BC
 =
=  …..(i) (By B.P. Theorem)
…..(i) (By B.P. Theorem)
and QE || AC
 =
=  …..(ii)
…..(ii)
∵ AD = BE (given) ……(iii)
AD + DE = BE + DE
AE = BD …..(iv)
putting values from equation (iii) and (iv) in (ii)
 =
=  =
= 
From equation (i) and (v)
 =
=  =
= 
⇒ =
= 
⇒ =
= 
⇒ PQ || AB
Point D and E lie on side AB of ∆ABC such that AD = BE. If DP || BC and EQ || AC then prove that PQ || AB.
Solution :
Given : ∆ABC in which
AD = BE,
DP || BC and EQ || AC
To prove PQ || AB

Proof : In ∆ABC DP || BC
and QE || AC
∵ AD = BE (given) ……(iii)
AD + DE = BE + DE
AE = BD …..(iv)
putting values from equation (iii) and (iv) in (ii)
From equation (i) and (v)
⇒
⇒
⇒ PQ || AB
Question 9.
ABCD is a Trapezium in which AB || DC and its diagonals intersects each other at point O. Show that :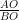 =
=  (Higher Secondary Board Raj 2012)
(Higher Secondary Board Raj 2012)

Solution :
Given : Trapezium ABCD in which AC and BC are two diagonals which intersects each other at point O.
To prove :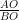 =
= 
Construction : From O, Draw OE || CD.
Proof : In ∆ADC
OE || DC
 =
=  ……(i) (By Basic prop. Theorem)
……(i) (By Basic prop. Theorem)
In Trapezium ABCD
AB || CD
OE || CD
OE || AB
Now, In ∆ABD
OE || AB
 =
= 
⇒ =
= 
From equation (i) and (ii)
 =
= 
⇒ AO × DO = BO × CO
⇒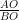 =
= 
ABCD is a Trapezium in which AB || DC and its diagonals intersects each other at point O. Show that :

Solution :
Given : Trapezium ABCD in which AC and BC are two diagonals which intersects each other at point O.
To prove :
Construction : From O, Draw OE || CD.
Proof : In ∆ADC
OE || DC
In Trapezium ABCD
AB || CD
OE || CD
OE || AB
Now, In ∆ABD
OE || AB
⇒
From equation (i) and (ii)
⇒ AO × DO = BO × CO
⇒
Question 10.
Points D and E lie on sides AB and AC of ∆ABC such that BD = CE then show that ∆ABC Is isosceles triangles.
Solution :
Given : In ∆ABC, D and E lie on sides AB and AC such that BD = CE.
To prove : ∆ABC is an isosceles triangle.

Construction : Join DC and BE.
Proof : In ∆BCD and ∆BEC
BD = CE (given)
∠BDC = ∠BEC [∵ angles of same base an some height]
BC = BC (common)
By SAS rule ∆BCD = ∆BEC
∴ ∠ABC = ∠ACE (by CPCT)
⇒ AB = AC (Sides opposite to equal angles are same)
Hence ∆ABC is an isosceles triangle.
Points D and E lie on sides AB and AC of ∆ABC such that BD = CE then show that ∆ABC Is isosceles triangles.
Solution :
Given : In ∆ABC, D and E lie on sides AB and AC such that BD = CE.
To prove : ∆ABC is an isosceles triangle.

Construction : Join DC and BE.
Proof : In ∆BCD and ∆BEC
BD = CE (given)
∠BDC = ∠BEC [∵ angles of same base an some height]
BC = BC (common)
By SAS rule ∆BCD = ∆BEC
∴ ∠ABC = ∠ACE (by CPCT)
⇒ AB = AC (Sides opposite to equal angles are same)
Hence ∆ABC is an isosceles triangle.






0 Comments