Chapter 11 Similarity Ex 11.4

Rajasthan Board RBSE Class 10 Maths Chapter 11 Similarity Ex 11.4

Question 1.
Answer the following in True of False. And justify your answer of possible :
(i) Ratio of corresponding sides of two similar triangles is 4 : 9 then ratio of areas of these triangles is 4 : 9.
(ii) In the triangles ABC and DEF if

then ∆ABC = ∆DEF
(iii) The ratio of areas of two similar triangles is proportional to square of their sides.
(iv) If ∆ABC and ∆AXY are similar and their areas are equal then sides XY and BC may coincides.
Solution :

Ratio of corresponding sides are 3 : 2 where s for similarity its ratio is 1 : 1
So this statement is wrong.
(iii) Ratio of areas of two similar triangles is equal to ratio of square of their corresponding sides.
Thus statement is false.
(iv) ∆ABC ~ ∆AXY

Similarly BC = XY and AC = AY
Thus, statement is true.

Question 2.
If ∆ABC ~ ∆DEF and their areas are 64 cm2 and 121 cm2 respectively. If EF = 15.4 cm
Solution :
∵ ∆ABC ~ ∆DEF (given)
∴ Ratio of areas of ∆
= ratio of squares of corresponding sides ∆

Question 3.
In the following figure, two triangles ABC and DBC are formed on same base BC. If AD, BC intersect at point O then show that
 = 
Solution :
Given : ∆ABC and ∆DBC are two triangles on same base BC. AD, BC intersects each other at point O.

To prove :  = 
Construction : From vertices A and D draw AE ⊥ BC and DE ⊥ BC respectively.
Proof : From vertices A and D, AE ⊥ BC and DF ⊥ BC.
∴ ∠AEO = ∠DFO = 90°
In right angled ∆AEO and ∆DFO
∠AEO = ∠DFO (each 90°)
∠AOE = ∠DOF (vertically opposite angles)
By A-A Similarity criterion
∆AEO – ∆DFO
⇒  = 
Now area of ∆ABC =  BC × AE
and area of ∆DBC =  BC × DF

from equation (i) and (ii)
 = 

Question 4.
Solve the following questions :
(i) In ∆ABC and DE || BC and AD : DB = 2 : 3 then find the ratio of areas of ∆ADE and ∆ABC.
(ii) PB and PA are perpendicular at A and B of line segment AB. If P and Q lies on two sides AB and by joining P and Q. It intersects AB at O and PD = 5 cm, QO = 7 cm, ar(∆POB) = 150 cm2 then find ar(∆QOA).
(iii) In figure, find x is terms of a, b and c

Solution :
(i) In ∆ABC BC || DE and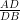  =  (given)
In ∆ABC and ∆DEA
∠B = ∠D
∠C = ∠E

A-A Similarity criterion


Thus,  = 
(ii) In ∆AOQ and ∆BOP
∠A = ∠B = 90° (given)
∠AOQ = ∠POB (vertically opposite angle)

(iii) ∠A = ∠B = 50° (corresponding angles)
∴ AE || BD

In ∆BDC and ∆AEC
∠A = ∠B = 50° (given)
∠E = ∠D (corresponding angles)
By AA similarity criterion
∆BDC ~ ∆AEC
∴  = 
⇒  = 
⇒ x = 

Question 5.
In ∆ABC, ∠B = 90° and BD is perpendicular to hypotenuse AC then prove that
∆ADB ~ ∆BDC
Solution :
Given : In ∆ABC ∠B = 90° and BD ⊥ AC
To prove : ∆ADB ~ ∆BDC

In ∆ABC
∠A + ∠C = 90° [∵ ∠B = 90°] …..(i)
In ∆BDC
∠DBC + ∠C = 90° [∵ ∠BDC = 90°] ……(ii)
From equation (i) and (ii)
∠A + ∠C = ∠DBC + ∠C
⇒ ∠A = ∠DBC …(iii)
Now, In ∆ADB and ∆BDC
∠ADB = ∠BDC = 90° (given)
∠DAB = ∠DBC (by eqn(iii))
By A-A Similarly criterion
∆ADB ~ ∆BDC

Question 6.
Prove that area of an equilateral triangle formed any side of a square is half the area of an equilateral triangle formed at the diagonal of same square.
Solution :
Given : ABCD is a square whose our side is AB and diagonal is AC. An equilateral triangles ABE and ACE are formed on the sides AB and AC respectively.

To prove :
ar. (∆ABE) = ar. (∆ACF)
Proof : In right angle ∆ABC
AC² = AB² + BC² (By Pythagoras theorem)
AC² = AB² + AB² (∵ BC = AB)
AC² = 2AB²
∴ AC =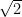  AB
Area of equilateral ∆ABE formed on side AB.
= 
and area of equilateral ∆ACF formed on hypotenuse AC.

Thus (∆ABE) =  ar.(∆ACF)