Rajasthan Board RBSE Class 10 Maths Chapter 11 Similarity Miscellaneous Exercise
Question 1.
In fig. DE || BC, AD = 4 cm, DB = 6 cm and AE = 5 cm then EC will be :

(A) 6.5 cm
(B) 7.0 cm
(C) 7.5 cm
(D) 8.0 cm
Solution :
AD = 4 cm
AE = 5 cm
BD = 6 cm
In ∆ABC
BC || DE
∴ =
=  (By Basic Prop. Theorem)
(By Basic Prop. Theorem)

⇒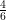 =
= 
⇒ CE =
⇒ CE = 7.5 cm
Hence option (C) is correct.
In fig. DE || BC, AD = 4 cm, DB = 6 cm and AE = 5 cm then EC will be :

(A) 6.5 cm
(B) 7.0 cm
(C) 7.5 cm
(D) 8.0 cm
Solution :
AD = 4 cm
AE = 5 cm
BD = 6 cm
In ∆ABC
BC || DE
∴

⇒
⇒ CE =
⇒ CE = 7.5 cm
Hence option (C) is correct.
Question 2.
In fig. AD is bisector of ∠A, AB = 6 cm, BD = 8 cm, DC = 6 cm, then AC will be :

(A) 4.0 cm
(B) 4.5 cm
(C) 5 cm
(D) 5.5 cm
Solution :
In ∆ABC
AD is bisector of ∠A
∴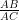 =
=  (By Basic Prop. Theorem)
(By Basic Prop. Theorem)
⇒ =
= 
⇒ 8 AC = 6 × 6
⇒ AC =
AC = 4.5 cm
Thus, (B) is correct option.
In fig. AD is bisector of ∠A, AB = 6 cm, BD = 8 cm, DC = 6 cm, then AC will be :

(A) 4.0 cm
(B) 4.5 cm
(C) 5 cm
(D) 5.5 cm
Solution :
In ∆ABC
AD is bisector of ∠A
∴
⇒
⇒ 8 AC = 6 × 6
⇒ AC =
AC = 4.5 cm
Thus, (B) is correct option.
Question 3.
In fig. it DE || BC then x will be :

(A)
(B)
(C)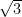
(D)
Solution :
In ΔABC
DE || BC
∴ =
= 
⇒ =
=  (By cross multiplication method)
(By cross multiplication method)
⇒ (x + 4)(x + 1) = (x + 3)(2x – 1)
⇒ x2 + 4x + x + 4 = 2x2 – x + 6x – 3
⇒ x2 + 5x + 4 = 2x2 + 5x – 3
⇒ x2 = 7
⇒ x = ±
Negative value of x is not possible.
∴ x =
Thus (D) is correct.
In fig. it DE || BC then x will be :

(A)
(B)
(C)
(D)
Solution :
In ΔABC
DE || BC
∴
⇒
⇒ (x + 4)(x + 1) = (x + 3)(2x – 1)
⇒ x2 + 4x + x + 4 = 2x2 – x + 6x – 3
⇒ x2 + 5x + 4 = 2x2 + 5x – 3
⇒ x2 = 7
⇒ x = ±
Negative value of x is not possible.
∴ x =
Thus (D) is correct.
Question 4.
In fig. if AB = 34 cm, BD = 4 cm, BC = 10 cm

(A) 5.1 cm
(B) 3.4 cm
(C) 6 cm
(D) 5.3 cm
Solution :
In ΔABC
AD is bisector of vertex angle A.
∴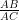 =
= 
⇒ =
= 
⇒ =
= 
⇒ =
= 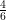
⇒ AC =
⇒ AC = 5.1 cm
Thus (A) is correct option.
In fig. if AB = 34 cm, BD = 4 cm, BC = 10 cm

(A) 5.1 cm
(B) 3.4 cm
(C) 6 cm
(D) 5.3 cm
Solution :
In ΔABC
AD is bisector of vertex angle A.
∴
⇒
⇒
⇒
⇒ AC =
⇒ AC = 5.1 cm
Thus (A) is correct option.
Question 5.
The areas of two similar triangle are 25 cm2 and 36 cm2 respectively. If median of smaller triangle be 10 cm then corresponding median of larger triangle will be :
(A) 12 cm
(B) 15 cm .
(C) 10 cm
(D) 18 cm
Solution :
We know that areas of two similar triangles is equal to the ratio of squares of their corresponding medians :

Thus (A) is correct option.
The areas of two similar triangle are 25 cm2 and 36 cm2 respectively. If median of smaller triangle be 10 cm then corresponding median of larger triangle will be :
(A) 12 cm
(B) 15 cm .
(C) 10 cm
(D) 18 cm
Solution :
We know that areas of two similar triangles is equal to the ratio of squares of their corresponding medians :

Thus (A) is correct option.
Question 6.
In a trapezium ABCD, AB || CD and the diagonals meet at point O. If AB = 6 cm and DC = 3 cm, then ratio of ar (∆AOB) and ar(∆COD) will be :
(A) 4 : 1
(B) 1 : 2
(C) 2 : 1
(D) 1 : 4
Solution :
∆AOB and ∆COD
∠AOB = ∠COD (Vertically opposite angles)
AB || CD
∠ABO = ∠CDO (Alternate angles)

By A-A similarity
ΔAOB ~ ΔCOD
We know that ratio of two similar triangles is equal to ratio- of squares of their corresponding sides.
Thus,
⇒
⇒ =
= 
⇒ =
= 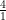
⇒ = 4 : 1
= 4 : 1
Thus, required raito will be 4 : 1.
Thus (A) is correct option.
In a trapezium ABCD, AB || CD and the diagonals meet at point O. If AB = 6 cm and DC = 3 cm, then ratio of ar (∆AOB) and ar(∆COD) will be :
(A) 4 : 1
(B) 1 : 2
(C) 2 : 1
(D) 1 : 4
Solution :
∆AOB and ∆COD
∠AOB = ∠COD (Vertically opposite angles)
AB || CD
∠ABO = ∠CDO (Alternate angles)

By A-A similarity
ΔAOB ~ ΔCOD
We know that ratio of two similar triangles is equal to ratio- of squares of their corresponding sides.
Thus,
⇒
⇒
⇒
⇒
Thus, required raito will be 4 : 1.
Thus (A) is correct option.
Question 7.
If in ∆ABC and ∆DEF ∠A = 50°, ∠B = 70°, ∠C = 60°, ∠D = 60°, ∠E = 70°, and ∠F = 50° then which one is correct ?
(A) ∆ABC ~ ∆DEF
(B) ∆ABC ~ ∆EDF
(C) ∆ABC ~ ∆DEF
(D) ∆ABC ~ ∆FED

Solution :
∠A = ∠F = 50°
∠B = ∠E = 70°
∠C = ∠D = 60°
∴ ∆ABC ~ ∆FED
Thus, option (D) is correct.
If in ∆ABC and ∆DEF ∠A = 50°, ∠B = 70°, ∠C = 60°, ∠D = 60°, ∠E = 70°, and ∠F = 50° then which one is correct ?
(A) ∆ABC ~ ∆DEF
(B) ∆ABC ~ ∆EDF
(C) ∆ABC ~ ∆DEF
(D) ∆ABC ~ ∆FED

Solution :
∠A = ∠F = 50°
∠B = ∠E = 70°
∠C = ∠D = 60°
∴ ∆ABC ~ ∆FED
Thus, option (D) is correct.
Question 8.
If ∆ABC ~ ∆DEF and AB = 10 cm then ar (∆ABC) will be ar (∆DEF).
(A) 25 : 16
(B) 16 : 25
(C) 4 : 5
(D) 5 : 4
Solution : ∆ABC ~ ∆DEF

=
=
ar. (∆ABC) : ar.(∆DEF) = 25 : 16
Hence (A) is correct.
If ∆ABC ~ ∆DEF and AB = 10 cm then ar (∆ABC) will be ar (∆DEF).
(A) 25 : 16
(B) 16 : 25
(C) 4 : 5
(D) 5 : 4
Solution : ∆ABC ~ ∆DEF
=
=
ar. (∆ABC) : ar.(∆DEF) = 25 : 16
Hence (A) is correct.
Question 9.
The point D and E lies on sides AB and AC of ∆ABC such that DE || BC and AD = 8 cm, AB = 12 cm and AE = 12 cm, then CE will be :
(A) 6 cm
(B) 18 cm
(C) 9 cm
(D) 15 cm

Solution :
In ∆ABC
DE || BC
∴ =
=  (Basic Prop. Theorem)
(Basic Prop. Theorem)
 =
= 
⇒ =
= 
⇒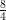 =
= 
⇒ 8 × CE = 12 × 4
⇒ CE =
⇒ CE = 6 cm
Thus (A) is correct option.
The point D and E lies on sides AB and AC of ∆ABC such that DE || BC and AD = 8 cm, AB = 12 cm and AE = 12 cm, then CE will be :
(A) 6 cm
(B) 18 cm
(C) 9 cm
(D) 15 cm

Solution :
In ∆ABC
DE || BC
∴
⇒
⇒
⇒ 8 × CE = 12 × 4
⇒ CE =
⇒ CE = 6 cm
Thus (A) is correct option.
Question 10.
The shadow of a 12 m long vertical rod on earth is 8 cm long. At the same time if shadow of tower in 40 m long, then height of pillar will be :
(A) 60 m
(B) 60 cm
(C) 40 cm
(D) 80 cm
Solution :
Let AB is vertical rod and BC is its shadow PQ is tower and CQ is its shadow.

In ∆ABC and ∆PQC
∠ACB = ∠PCQ (Common)
∠ABC = ∠PQC (each 90°)
By AA similarity criterion
∆ABC ~ ∆PQC
∴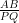 =
=  (∵ corresponding sides os similar triangle are proportional)
(∵ corresponding sides os similar triangle are proportional)
⇒ =
= 
∴ PQ =
= 5 × 12 = 60 m
Thus, (A) is correct.
The shadow of a 12 m long vertical rod on earth is 8 cm long. At the same time if shadow of tower in 40 m long, then height of pillar will be :
(A) 60 m
(B) 60 cm
(C) 40 cm
(D) 80 cm
Solution :
Let AB is vertical rod and BC is its shadow PQ is tower and CQ is its shadow.

In ∆ABC and ∆PQC
∠ACB = ∠PCQ (Common)
∠ABC = ∠PQC (each 90°)
By AA similarity criterion
∆ABC ~ ∆PQC
∴
⇒
∴ PQ =
= 5 × 12 = 60 m
Thus, (A) is correct.
Question 11.
If in ΔABCD, is any point on BC such that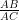 =
=  and ∠B = 70°, ∠C = 50°, then find ∠BAD.
and ∠B = 70°, ∠C = 50°, then find ∠BAD.
Solution :
In ∆ABC
∠B = 70°, ∠C = 50° (given)

∴ ∠A + ∠B + ∠C = 180°
⇒ ∠A = 180° – (∠B + ∠C)
⇒ ∠A = 180° – (70° + 50°)
⇒ ∠A = 180° – 120°
⇒ ∠A = 60°
Thus,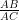 =
=  (given)
(given)
∴ ∆ABD ~ ∆ADC
⇒ ∠BAD and ∠DAC will be equal to each other.
2∠BAD = 60°
∠BAD =
∠BAD = 30°
If in ΔABCD, is any point on BC such that
Solution :
In ∆ABC
∠B = 70°, ∠C = 50° (given)

∴ ∠A + ∠B + ∠C = 180°
⇒ ∠A = 180° – (∠B + ∠C)
⇒ ∠A = 180° – (70° + 50°)
⇒ ∠A = 180° – 120°
⇒ ∠A = 60°
Thus,
∴ ∆ABD ~ ∆ADC
⇒ ∠BAD and ∠DAC will be equal to each other.
2∠BAD = 60°
∠BAD =
∠BAD = 30°
Question 12.
In, ∆ABC DE || BC and AD = 6 cm, DE = 9 cm and AE = 8 cm, then find AC.
Solution :
In ∆ABC
DE || BC
∴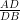 =
=  (By Basic Theorem)
(By Basic Theorem)

⇒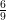 =
= 
⇒ 6 × CE = 9 × 8
⇒ CE =
⇒ CE = 12 cm
∴ AC = AE + CE
= (8 + 12) cm
= 20 cm
Thus, AC = 20 cm
In, ∆ABC DE || BC and AD = 6 cm, DE = 9 cm and AE = 8 cm, then find AC.
Solution :
In ∆ABC
DE || BC
∴

⇒
⇒ 6 × CE = 9 × 8
⇒ CE =
⇒ CE = 12 cm
∴ AC = AE + CE
= (8 + 12) cm
= 20 cm
Thus, AC = 20 cm
Question 13.
In ∆ABC if AD of is bisector of ∠A and AB = 8 cm, BD = 5 cm and DC = 4 cm. then find AC.
Solution :
In ∆ABC
AD, bisect vertex angle A

∴ ∠BAD = ∠CAD
∴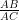 =
= 
⇒ =
= 
⇒ 5 AC = 8 × 4
⇒ AC =
⇒ AC = 6.4 cm
In ∆ABC if AD of is bisector of ∠A and AB = 8 cm, BD = 5 cm and DC = 4 cm. then find AC.
Solution :
In ∆ABC
AD, bisect vertex angle A

∴ ∠BAD = ∠CAD
∴
⇒
⇒ 5 AC = 8 × 4
⇒ AC =
⇒ AC = 6.4 cm
Question 14.
If heights of two triangles are in the ratio 4 : 9, then find the ratio of their areas.
Solution :
We know that ratio of areas of two similar triangles is equal to the ratio of square of their corresponding heights.

Let ∆ABC and ∆DEF are similar and AE and DN are their corresponding heights.
∴ Ratio of the area of two triangle will be 16 : 81.
If heights of two triangles are in the ratio 4 : 9, then find the ratio of their areas.
Solution :
We know that ratio of areas of two similar triangles is equal to the ratio of square of their corresponding heights.

Let ∆ABC and ∆DEF are similar and AE and DN are their corresponding heights.
∴ Ratio of the area of two triangle will be 16 : 81.






0 Comments