RBSE Solutions for Class 10 Maths Chapter 6 Trigonometric Ratios Ex 6.1.
Class 10 Maths Chapter 6 Trigonometric Ratios Ex 6.1. solution. Solution is provided in this post. Here we have provide the solutions of RBSE Boards Books according to chapter wise.
 |
| Chapter 6 Trigonometric Ratios Ex 6.1. |
RBSE Solutions for Class 10 Maths Chapter 6 Trigonometric Ratios Ex 6.1.
Find the value of the following : (Q. 1 to 10)
Question 1.
2 sin 45° cos 45°
Solution :
2 sin 45° cos 45° = 2 ×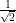 ×
× 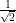
= 2 × = 1
= 1
Question 1.
2 sin 45° cos 45°
Solution :
2 sin 45° cos 45° = 2 ×
= 2 ×
Question 2.
cos 45° cos 60° – sin 45° sin 60°.
Solution :
cos 45° cos 60° – sin 45° sin 60°

cos 45° cos 60° – sin 45° sin 60°.
Solution :
cos 45° cos 60° – sin 45° sin 60°

 |
| Chapter 6 Trigonometric Ratios Ex 6.1. |
Question 3.
sin2 30° + 2 cos2 45° + 3 tan2 60°
Solution :
sin2 30° + 2 cos2 45° + 3 tan2 60°
Putting value of trigonometric ratios,

sin2 30° + 2 cos2 45° + 3 tan2 60°
Solution :
sin2 30° + 2 cos2 45° + 3 tan2 60°
Putting value of trigonometric ratios,

Question 4.
3 sin 60° – 4 sin3 60°.
Solution :
3 sin 60° – 4 sin3 60°
Putting value of trigonometric ratios

3 sin 60° – 4 sin3 60°.
Solution :
3 sin 60° – 4 sin3 60°
Putting value of trigonometric ratios

Question 5.

Solution :


Solution :

 |
| Chapter 6 Trigonometric Ratios Ex 6.1. |
Question 6.
4 cot2 45° – sec2 60° + sin2 60° + cos2 90°.
Solution :
4 cot2 45° – sec2 60° + sin2 60° + cos2 90°

4 cot2 45° – sec2 60° + sin2 60° + cos2 90°.
Solution :
4 cot2 45° – sec2 60° + sin2 60° + cos2 90°

Question 7.

Solution :


Solution :

Question 8.

Solution :


Solution :

 |
| Chapter 6 Trigonometric Ratios Ex 6.1. |
Question 9.

Solution :

Question 10.

Solution :


Solution :

 |
| Chapter 6 Trigonometric Ratios Ex 6.1. |
Question 11.
Find the value of x in the following :
(i) cos x = cos 60° cos 30° + sin 60° sin 30°
(ii) sin 2x = sin 60° cos 30° – cos 60° sin 30°
(iii) √3 tan2x = sin 30° + sin 45° cos 45° + 2 sin 90°.
Solution :
(i) cos x = cos 60° cos 30° + sin 60° sin 30°

cos x = cos 30°
x = 30°
(ii) sin 2x = sin 60° cos 30° – cos 60° sin 30°

⇒ sin 2x = = sin 30°
= sin 30°
⇒ 2x = 30° ⇒ x = 15°
(iii) √3 tan2x = sin 30° + sin 45° cos 45° + 2 sin 90°

√3 tan2x = 3
⇒ tan 2x =
⇒ tan 2x = √3
⇒ tan 2x = tan 60°
⇒ 2x = 60°
⇒ x = 30°
Find the value of x in the following :
(i) cos x = cos 60° cos 30° + sin 60° sin 30°
(ii) sin 2x = sin 60° cos 30° – cos 60° sin 30°
(iii) √3 tan2x = sin 30° + sin 45° cos 45° + 2 sin 90°.
Solution :
(i) cos x = cos 60° cos 30° + sin 60° sin 30°

cos x = cos 30°
x = 30°
(ii) sin 2x = sin 60° cos 30° – cos 60° sin 30°

⇒ sin 2x =
⇒ 2x = 30° ⇒ x = 15°
(iii) √3 tan2x = sin 30° + sin 45° cos 45° + 2 sin 90°

√3 tan2x = 3
⇒ tan 2x =
⇒ tan 2x = √3
⇒ tan 2x = tan 60°
⇒ 2x = 60°
⇒ x = 30°
Prove that : (Q. 12 to Q. 20)
Question 12.

Solution :
L.H.S.

Question 12.

Solution :
L.H.S.

= R.H.S.
 |
| Chapter 6 Trigonometric Ratios Ex 6.1. |
Question 13.
4 cot2 45° – sec2 60° – sin2 30° = –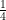
Solution :
4 cot2 45° – sec2 60° – sin2 30° = –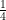
L.H.S. = 4 cot2 45° – sec2 60° – sin2 30°
= 4(1)2 – (2)2 – { \left( \frac { 1 }{ 2 } \right) }^{ 2 }
= 4 – 4 –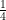 = –
= –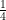
= R.H.S.
Hence, L.H.S. = R.H.S.
4 cot2 45° – sec2 60° – sin2 30° = –
Solution :
4 cot2 45° – sec2 60° – sin2 30° = –
L.H.S. = 4 cot2 45° – sec2 60° – sin2 30°
= 4(1)2 – (2)2 – { \left( \frac { 1 }{ 2 } \right) }^{ 2 }
= 4 – 4 –
= R.H.S.
Hence, L.H.S. = R.H.S.
Question 14.
4 sin 30° sin2 60° + 3 cos 60° tan 45° = 2 sec2 45° – cosec2 90°
Solution :
L.H.S. = 4 sin 30° sin2 60° + 3 cos 60° tan 45°
Putting values of trigonometric ratios,

R.H.S. = 2 sec2 45° – cosec2 90°
Putting values of trigonometric ratios,
= 2(√2)2 – (1)2 = 4 – 1 = 3
∴ L.H.S. = R.H.S.
4 sin 30° sin2 60° + 3 cos 60° tan 45° = 2 sec2 45° – cosec2 90°
Solution :
L.H.S. = 4 sin 30° sin2 60° + 3 cos 60° tan 45°
Putting values of trigonometric ratios,

R.H.S. = 2 sec2 45° – cosec2 90°
Putting values of trigonometric ratios,
= 2(√2)2 – (1)2 = 4 – 1 = 3
∴ L.H.S. = R.H.S.
Question 15.
cosec2 45° sec2 30° sin3 90° cos 60° =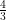
Solution :
L.H.S. = cosec2 45° sec2 30° sin3 90° cos 60°

∴ L.H.S. = R.H.S.
cosec2 45° sec2 30° sin3 90° cos 60° =
Solution :
L.H.S. = cosec2 45° sec2 30° sin3 90° cos 60°

∴ L.H.S. = R.H.S.
 |
| Chapter 6 Trigonometric Ratios Ex 6.1. |
Question 16.

Solution :
L.H.S.


Thus, L.H.S. = R.H.S.

Solution :
L.H.S.


Thus, L.H.S. = R.H.S.
Question 17.
2(cos2 45° + tan2 60°) – 6(sin2 45° – tan2 30°) = 6
Solution :
2(cos2 45° + tan2 60°) – 6(sin2 45° – tan2 30°)

= 7 – 1 = 6
Thus, 2(cos2 45° + tan2 60°) – 6(sin2 45° – tan2 30°) = 6
2(cos2 45° + tan2 60°) – 6(sin2 45° – tan2 30°) = 6
Solution :
2(cos2 45° + tan2 60°) – 6(sin2 45° – tan2 30°)

= 7 – 1 = 6
Thus, 2(cos2 45° + tan2 60°) – 6(sin2 45° – tan2 30°) = 6
Question 18.
(sec2 30° + cosec2 45°) (2 cos 60°+ sin 90° + tan 45°) = 10
Solution :
(sec2 30° + cosec2 45°) (2 cos 60°+ sin 90° + tan 45°)

Thus, (sec2 30° + cosec2 45°) (2 cos 60°+ sin 90° + tan 45°) = 10.
(sec2 30° + cosec2 45°) (2 cos 60°+ sin 90° + tan 45°) = 10
Solution :
(sec2 30° + cosec2 45°) (2 cos 60°+ sin 90° + tan 45°)

Thus, (sec2 30° + cosec2 45°) (2 cos 60°+ sin 90° + tan 45°) = 10.
 |
| Chapter 6 Trigonometric Ratios Ex 6.1. |
Question 19.
(1 – sin 45° + sin 30°) (1 + cos 45° + cos 60°) =
Solution :
(1 – sin 45° + sin 30°) (1 + cos 45° + cos 60°)


Thus, (1 – sin 45° + sin 30°) (1 + cos 45° + cos 60°) =
(1 – sin 45° + sin 30°) (1 + cos 45° + cos 60°) =
Solution :
(1 – sin 45° + sin 30°) (1 + cos 45° + cos 60°)


Thus, (1 – sin 45° + sin 30°) (1 + cos 45° + cos 60°) =
Question 20.
cos2 0° – 2 cot2 30° + 3 cosec2 90° = 2(sec2 45° – tan2 60°)
Solution :
L.H.S. = cos2 0° – 2 cot2 30° + 3 cosec2 90°
= (1)2 – 2(√3)2 + 3(1)2
= 1 – 2 × 3 + 3
= 1 – 6 + 3 = -2
R.H.S. = 2(sec2 45° – tan2 60°)
= 2[(√2)2 – (√3)2]
= 2(2 – 3) = 2 × (-1) = -2
Thus, L.H.S. = R.H.S.
Question 21.
If x = 30°, then prove that
(i) sin 3x = 3 sin x – 4 sin3 x

(iv) cos 3x = 4 cos3 x – 3 cos x
Solution :
(i) sin 3x = 3 sin x – 4 sin3 x
L.H.S. = sin 3x
= sin 3 × 30° [∵ Given x = 30°]
= sin 90°
= 1
R.H.S. = 3 sin x – 4 sin3 x
= 3sin 30° – 4 sin3 30°

Thus, L.H.S. = R.H.S.
If x = 30°, then prove that
(i) sin 3x = 3 sin x – 4 sin3 x

(iv) cos 3x = 4 cos3 x – 3 cos x
Solution :
(i) sin 3x = 3 sin x – 4 sin3 x
L.H.S. = sin 3x
= sin 3 × 30° [∵ Given x = 30°]
= sin 90°
= 1
R.H.S. = 3 sin x – 4 sin3 x
= 3sin 30° – 4 sin3 30°

Thus, L.H.S. = R.H.S.
 |
| Chapter 6 Trigonometric Ratios Ex 6.1. |
(ii) tan 2x =
L.H.S. = tan 2x
= tan 2 × 30° [∵ Given x = 30°]
= tan 60° = √3
R.H.S. =

∴ L.H.S. = R.H.S.
(iii)

∴ L.H.S. = R.H.S.
(iv) cos 3x = 4 cos3 x – 3 cos x
L.H.S. = cos 3x = cos 3 × 30°
= cos 90°
= 0 [∵ Given x = 30°]
R.H.S. = 4 cos3 x – 3 cos x = 4 cos3 30° – 3 cos 30°

L.H.S. = R.H.S.
Question 22.
If A = 60° and B = 30° then prove that :
cot (A – B) =
Solution :
cot (A – B) =
∴ A = 60°, B = 30°
L.H.S. = cot(A-B) = cot(60° – 30°)
= cot 30° = √3
R.H.S. =

L.H.S. = R.H.S.
If A = 60° and B = 30° then prove that :
cot (A – B) =
Solution :
cot (A – B) =
∴ A = 60°, B = 30°
L.H.S. = cot(A-B) = cot(60° – 30°)
= cot 30° = √3
R.H.S. =

L.H.S. = R.H.S.
 |
| Chapter 6 Trigonometric Ratios Ex 6.1. |
Hope that the Solutions provided here for Class 10 Maths Chapter 6 Trigonometric Ratios Ex 6.1. will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 6 Trigonometric Ratios Ex 6.1. solution drop a comment below and like and share the post.
Thank you.






0 Comments