RBSE Solutions for Class 10 Maths Chapter 3 Polynomials Ex 3.5.
Class 10 Maths Chapter 3 Polynomials Ex 3.5 Solution is provided in this post. Here we have provide the solutions of RBSE Boards Books according to chapter wise.
 |
| Chapter 3 Polynomial Ex.3.5 solution. |
Rajasthan Board RBSE Class 10 Maths Chapter 3 Polynomials Ex 3.5.
 |
| Chapter 3 Polynomial Ex.3.5 solution. |
Question 1.
Find the nature of roots of following quadratic equations.
(i) 2x2 – 3x + 5 = 0
(ii) 2x2 – 4x + 3 = 0
(iii) 2x2 + x – 1 = 0
(iv) x2 – 4x + 4 = 0
(v) 2x2 + 5x + 5 = 0
(vi) 3x2 – 2x +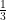 = 0
= 0
Solution
(i) Given equation 2x2 – 3x + 5 = 0
Comparing with ax2 + bx + c = 0
a = 2, b = – 3 and c = 5
Discriminant (D) = b2 – 4ac
= (-3)2 – 4 × 2 × 5
= 9 – 40
= -31 < 0
Thus given equation has no real roots.
(ii) Given equation
2x2 – 4x + 3 =0
Comparing it with ax2 + bx + c = 0
a = 2, b = – 4 and c = 3
Discriminant(D) = b2 – 4ac
= (-4)2 – 4 × 2 × 3
= 16 – 24
= -8 < 0
Thus given equation has no real roots.
(iii) Given equation 2x2 + x – 1 = 0
Comparing it with ax2 + bx + c = 0
a = 2, b = 1 and c = – 1
Discriminant (D) = b2 – 4ac
= (1)2 – 4 × 2 × (-1)
= 1 + 8
= 9 > 0
Hence, roots of equation are real and distinct
(iv) Given equation x2 – 4x + 4 = 0
Comparing it with quadratic equation ax2 + bx + c = 0
a = 1, b = -4 and c = 4
Discriminant (D) = b2 – 4ac
= (-4)2 – 4 × 1 × 4
= 16 – 16
= 0
Hence, roots of equation will be real and equal.
(v) Given equation 2x2 + 5x + 5 = 0
Comparing it with quadratic equation ax2 + bx + c = 0
a = 2, b = 5 and c = 5
Discriminant (D) = (5)2 – 4 × 2 × 5
= 25 – 40
= -15 < 0
Thus, roots of equation are not real.
(vi) Given equation 3x2 – 2x +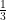 = o
= o
Comparing it by general quadratic equation
a = 3, b = -2, c =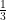
Discriminant (D) = b2 – 4ac
= (-2)2 – 4 × 3 ×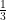
= 4 – 4
= 0
Hence, root of given equation are real and equal.
Find the nature of roots of following quadratic equations.
(i) 2x2 – 3x + 5 = 0
(ii) 2x2 – 4x + 3 = 0
(iii) 2x2 + x – 1 = 0
(iv) x2 – 4x + 4 = 0
(v) 2x2 + 5x + 5 = 0
(vi) 3x2 – 2x +
Solution
(i) Given equation 2x2 – 3x + 5 = 0
Comparing with ax2 + bx + c = 0
a = 2, b = – 3 and c = 5
Discriminant (D) = b2 – 4ac
= (-3)2 – 4 × 2 × 5
= 9 – 40
= -31 < 0
Thus given equation has no real roots.
(ii) Given equation
2x2 – 4x + 3 =0
Comparing it with ax2 + bx + c = 0
a = 2, b = – 4 and c = 3
Discriminant(D) = b2 – 4ac
= (-4)2 – 4 × 2 × 3
= 16 – 24
= -8 < 0
Thus given equation has no real roots.
(iii) Given equation 2x2 + x – 1 = 0
Comparing it with ax2 + bx + c = 0
a = 2, b = 1 and c = – 1
Discriminant (D) = b2 – 4ac
= (1)2 – 4 × 2 × (-1)
= 1 + 8
= 9 > 0
Hence, roots of equation are real and distinct
(iv) Given equation x2 – 4x + 4 = 0
Comparing it with quadratic equation ax2 + bx + c = 0
a = 1, b = -4 and c = 4
Discriminant (D) = b2 – 4ac
= (-4)2 – 4 × 1 × 4
= 16 – 16
= 0
Hence, roots of equation will be real and equal.
(v) Given equation 2x2 + 5x + 5 = 0
Comparing it with quadratic equation ax2 + bx + c = 0
a = 2, b = 5 and c = 5
Discriminant (D) = (5)2 – 4 × 2 × 5
= 25 – 40
= -15 < 0
Thus, roots of equation are not real.
(vi) Given equation 3x2 – 2x +
Comparing it by general quadratic equation
a = 3, b = -2, c =
Discriminant (D) = b2 – 4ac
= (-2)2 – 4 × 3 ×
= 4 – 4
= 0
Hence, root of given equation are real and equal.
 |
| Chapter 3 Polynomial Ex.3.5 solution. |
Question 2.
Find value of k, for which following quadratic equations have real and equal roots.
(i) kx(x – 2) + 6 = 0
(ii) x2 – 2(k + 1)x + k2 = 0
(iii) 2x2 + kx + 3 = 0
(iv) (k + 1)x2 – 2(k – 1) x + 1 = 0
(v) (k + 4)x2 + (k + 1) x + 1 = 0
(vi) kx2 – 5x + k = 0
Solution
(i) Given equation kx(x – 2) + 6 = 0
or kx2 – 2kx + 6 = 0
Comparing it with ax2 + bx + c = 0
a = k, b = -2k and c = 6
Discriminant D = b2 – 4ac
= (-2k)2 – 4 × k × 6
= 4k2 – 24k
= 4k(k – 6)
For equal roots D = 0
4k(k – 6) = 0
⇒ k = 0 or k – 6 = 0
⇒ k = 0 or k = 6
For equal roots k = 6 because k = 0 is not possible.
(ii) Given equation
x2 – 2(k + 1)x + k2 = o
Comparing it with ax2 + bc + c = 0
a = 1, b = -2(k + 1) and c = k2
Discriminant D = b2 – 4ac
= {-2(k + 1)}2 – 4 × 1 × k2
= 4(k2 + 2k + 1) – 4k2
= 4k2 + 8k + 4 – 4k2
= 8k + 4
For equal roots D = 0
⇒ 8k + 4 = 0
⇒ 8k = -4
⇒ k =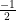
Thus k =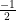
(iii) Given equation
2x2 + kr + 3 = 0
Comparing with ax2 + bx + c = 0
a = 2, b = k and c = 3
Discriminant D = b2 – 4ac
= k2 – 4 × 2 × 3
= k2 – 24
for equal roots D = 0
⇒ k2 – 24 = 0
⇒ k2 = 24
⇒ k = ±√24 = ±2√6
for equal roots k = ± 2√6
(iv) Given equation (k + 1)x2 – 2(k – 1)x + 1 = 0
Comparing it by ax2 + bx + c = 0
a = (k + 1), b = -2(k – 1) and c = 1
Discriminant, D = b2 – 4ac
= {-2 {k – 1)}2 – 4 × (k + 1) × 1
= 4{k2 + 1 – 2k) – 4 (k + 1)
= 4k2 + 4 – 8k – 4k – 4
= 4k2 – 12k
= 4k(k – 3)
for equal roots, D = 0
⇒ 4k(k – 3) = 0
⇒ k(k – 3) =0
⇒ k = 0 or k = 3
for equal roots k = 3, since k = 0
(v) Given equation is (k + 4)x2 + (k + 1)x + 1 = 0
Comparing it with ax2 + bx + c = 0
a = k + 4, b = k + 1, c = 1
Discriminant (D) = b2 – 4ac
= (k + 1 )2 – 4 × (k + 4) × 1
= k2 + 2k + 1 – 4k – 16
= k2 – 2k – 15
= k2 – 5k + 3k – 15
= k(k – 5) + 3(k – 5)
= (k – 5) (k + 3)
For equal roots, D = 0
⇒ (k – 5)(k + 3) = 0
⇒ k – 5 = 0 or k + 3 = 0
⇒ k = 5 or k = -3
(vi) Given equation kx2 – 5x + k = 0
Comparing it with ax2 + bx + c = 0
a = k, b = -5. c = k
Discriminant, (D) = b2 – 4ac
= (-5)2 – 4 × k × k
= 25 – 4k2
For equal roots D = 0

Find value of k, for which following quadratic equations have real and equal roots.
(i) kx(x – 2) + 6 = 0
(ii) x2 – 2(k + 1)x + k2 = 0
(iii) 2x2 + kx + 3 = 0
(iv) (k + 1)x2 – 2(k – 1) x + 1 = 0
(v) (k + 4)x2 + (k + 1) x + 1 = 0
(vi) kx2 – 5x + k = 0
Solution
(i) Given equation kx(x – 2) + 6 = 0
or kx2 – 2kx + 6 = 0
Comparing it with ax2 + bx + c = 0
a = k, b = -2k and c = 6
Discriminant D = b2 – 4ac
= (-2k)2 – 4 × k × 6
= 4k2 – 24k
= 4k(k – 6)
For equal roots D = 0
4k(k – 6) = 0
⇒ k = 0 or k – 6 = 0
⇒ k = 0 or k = 6
For equal roots k = 6 because k = 0 is not possible.
(ii) Given equation
x2 – 2(k + 1)x + k2 = o
Comparing it with ax2 + bc + c = 0
a = 1, b = -2(k + 1) and c = k2
Discriminant D = b2 – 4ac
= {-2(k + 1)}2 – 4 × 1 × k2
= 4(k2 + 2k + 1) – 4k2
= 4k2 + 8k + 4 – 4k2
= 8k + 4
For equal roots D = 0
⇒ 8k + 4 = 0
⇒ 8k = -4
⇒ k =
Thus k =
(iii) Given equation
2x2 + kr + 3 = 0
Comparing with ax2 + bx + c = 0
a = 2, b = k and c = 3
Discriminant D = b2 – 4ac
= k2 – 4 × 2 × 3
= k2 – 24
for equal roots D = 0
⇒ k2 – 24 = 0
⇒ k2 = 24
⇒ k = ±√24 = ±2√6
for equal roots k = ± 2√6
(iv) Given equation (k + 1)x2 – 2(k – 1)x + 1 = 0
Comparing it by ax2 + bx + c = 0
a = (k + 1), b = -2(k – 1) and c = 1
Discriminant, D = b2 – 4ac
= {-2 {k – 1)}2 – 4 × (k + 1) × 1
= 4{k2 + 1 – 2k) – 4 (k + 1)
= 4k2 + 4 – 8k – 4k – 4
= 4k2 – 12k
= 4k(k – 3)
for equal roots, D = 0
⇒ 4k(k – 3) = 0
⇒ k(k – 3) =0
⇒ k = 0 or k = 3
for equal roots k = 3, since k = 0
(v) Given equation is (k + 4)x2 + (k + 1)x + 1 = 0
Comparing it with ax2 + bx + c = 0
a = k + 4, b = k + 1, c = 1
Discriminant (D) = b2 – 4ac
= (k + 1 )2 – 4 × (k + 4) × 1
= k2 + 2k + 1 – 4k – 16
= k2 – 2k – 15
= k2 – 5k + 3k – 15
= k(k – 5) + 3(k – 5)
= (k – 5) (k + 3)
For equal roots, D = 0
⇒ (k – 5)(k + 3) = 0
⇒ k – 5 = 0 or k + 3 = 0
⇒ k = 5 or k = -3
(vi) Given equation kx2 – 5x + k = 0
Comparing it with ax2 + bx + c = 0
a = k, b = -5. c = k
Discriminant, (D) = b2 – 4ac
= (-5)2 – 4 × k × k
= 25 – 4k2
For equal roots D = 0

 |
| Chapter 3 Polynomial Ex.3.5 solution. |
Question 3.
Find value of k for which following quadratic equations have real and fractional roots.
(i) kx2 + 2x + 1 = 0
(ii) kx2 + 6x + 1 = 0
(iii) x2 – kx + 9 = 0
Solution
(i) Given roots kx2 + 2x + 1 = 0
Comparing it by general quadratic equation
ax2 + bx + c = 0
a = k, b = 2, c = 1
Discriminant (D) = b2 – 4ac
= (2)2 – 4 × k × 1
= 4 – 4 k
= 4(1 – k)
For real and fractional roots
Discriminant (D) > 0
⇒ 4(1 -k) > 0
⇒ 1 – k > 0
⇒ k < 1
Thus, k will be less than.
(ii) Given equation kx2 + 6x + 1 = 0
Comparing it by general quadratic equation ax2 + bx + c – 0,
a = k, b = 6, c = 1
Discriminant (D) = b2 – 4ac
= (6)2 – 4 × k × 1
= 36 – 4k
= 4(9 – k)
If discriminant (D) > 0 then roots of equation will be real and fractional.
i.e., D > 0
⇒ 4(9 – k) > 0
⇒ 9 – k > 0
⇒ k > 9
Thus value of k will be greater than 9
(iii) Given equation x2 – kx + 9 = 0
Comparing it by general quadratic equation
ax2 + bx + c = 0
a = 1, b = -k, c = 9
Discriminant (D) = b2 – 4ac
= (-k)2 – 4 × 1 × 9
= k2 – 36
If D > 0, then roots of equation will be real and fractional.
D > 0
⇒ k2 – 36 > 0
⇒ (k – 6)(k + 6) > 0
⇒ k – 6 > 0 or k + 6 > 0
⇒ k > 6 or k < -6
Thus, value of k will be greater than 6 or less than -6.
Find value of k for which following quadratic equations have real and fractional roots.
(i) kx2 + 2x + 1 = 0
(ii) kx2 + 6x + 1 = 0
(iii) x2 – kx + 9 = 0
Solution
(i) Given roots kx2 + 2x + 1 = 0
Comparing it by general quadratic equation
ax2 + bx + c = 0
a = k, b = 2, c = 1
Discriminant (D) = b2 – 4ac
= (2)2 – 4 × k × 1
= 4 – 4 k
= 4(1 – k)
For real and fractional roots
Discriminant (D) > 0
⇒ 4(1 -k) > 0
⇒ 1 – k > 0
⇒ k < 1
Thus, k will be less than.
(ii) Given equation kx2 + 6x + 1 = 0
Comparing it by general quadratic equation ax2 + bx + c – 0,
a = k, b = 6, c = 1
Discriminant (D) = b2 – 4ac
= (6)2 – 4 × k × 1
= 36 – 4k
= 4(9 – k)
If discriminant (D) > 0 then roots of equation will be real and fractional.
i.e., D > 0
⇒ 4(9 – k) > 0
⇒ 9 – k > 0
⇒ k > 9
Thus value of k will be greater than 9
(iii) Given equation x2 – kx + 9 = 0
Comparing it by general quadratic equation
ax2 + bx + c = 0
a = 1, b = -k, c = 9
Discriminant (D) = b2 – 4ac
= (-k)2 – 4 × 1 × 9
= k2 – 36
If D > 0, then roots of equation will be real and fractional.
D > 0
⇒ k2 – 36 > 0
⇒ (k – 6)(k + 6) > 0
⇒ k – 6 > 0 or k + 6 > 0
⇒ k > 6 or k < -6
Thus, value of k will be greater than 6 or less than -6.
 |
| Chapter 3 Polynomial Ex.3.5 solution. |
Question 4.
Find value of k, for which equation x2 + 5kx + 16 = 0 has no real roots.
Solution
Given equation x2 + 5kx + 16 = 0
Comparing it by general quadratic equation ax2 + bx + c = 0
a = 1, b = 5k, c = 16
Discriminant (D) = b2 – 4ac
= (5k)2 – 4 × 1 × 16
= 25k2 – 64
If Discriminant (D) < 0, then roots will not be real.
i.e. D < 0
⇒ 25k2 – 64 < 0
⇒ (5k – 8)(5k + 8) < 0
⇒ 5k – 8 < 0 or 5k + 8 < 0
⇒ k <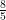 or k >
or k > 
Hence, value of k will be smaller than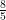 or greater than
or greater than  .
.
Find value of k, for which equation x2 + 5kx + 16 = 0 has no real roots.
Solution
Given equation x2 + 5kx + 16 = 0
Comparing it by general quadratic equation ax2 + bx + c = 0
a = 1, b = 5k, c = 16
Discriminant (D) = b2 – 4ac
= (5k)2 – 4 × 1 × 16
= 25k2 – 64
If Discriminant (D) < 0, then roots will not be real.
i.e. D < 0
⇒ 25k2 – 64 < 0
⇒ (5k – 8)(5k + 8) < 0
⇒ 5k – 8 < 0 or 5k + 8 < 0
⇒ k <
Hence, value of k will be smaller than
 |
| Chapter 3 Polynomial Ex.3.5 solution. |
Question 5.
If roots of quadratic equation (b – c)x2 + (c – a)x + (a – b) = 0 are real and equal, then prove that 2b = a + c
Solution
Given equation is (b – c)x2 + (c – a)x + (a – b) = 0
Comparing it by general quadratic equation, a = (b – c), b = (c – a) and c = (a – b)
Discriminant (D) = b2 – 4ac
= (c – a)2 – 4(b – c)(a – b)
= (c2 + a2 – 2ac) – 4(ab – ac – b2 + bc)
= c2 + a2 – 2ac – 4ab + 4ac + 4b2 – 4bc
= c2 + a2 + 2ac – 4ab – 4bc + 4b2
= (a + c)2 – 4 b(a + c) + 4b2
= (a + c)2 – 2 × (a + c) × 2b + (2b)2
= [(a + c) – 2b]2
Roots of equation are real and equal.
D = 0
⇒ [(a + c) – 2b]2 = 0
⇒ (a + c) – 2b = 0
⇒ a + c = 2b
Hence Proved.
If roots of quadratic equation (b – c)x2 + (c – a)x + (a – b) = 0 are real and equal, then prove that 2b = a + c
Solution
Given equation is (b – c)x2 + (c – a)x + (a – b) = 0
Comparing it by general quadratic equation, a = (b – c), b = (c – a) and c = (a – b)
Discriminant (D) = b2 – 4ac
= (c – a)2 – 4(b – c)(a – b)
= (c2 + a2 – 2ac) – 4(ab – ac – b2 + bc)
= c2 + a2 – 2ac – 4ab + 4ac + 4b2 – 4bc
= c2 + a2 + 2ac – 4ab – 4bc + 4b2
= (a + c)2 – 4 b(a + c) + 4b2
= (a + c)2 – 2 × (a + c) × 2b + (2b)2
= [(a + c) – 2b]2
Roots of equation are real and equal.
D = 0
⇒ [(a + c) – 2b]2 = 0
⇒ (a + c) – 2b = 0
⇒ a + c = 2b
Hence Proved.
Hope that the Solutions provided here for Class 10 Maths Chapter 3 Polynomials Ex 3.5 will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 3 Polynomials Exercise 3.5 drop a comment below and like and share the post.
Thank you.






0 Comments