Chapter 3 Polynomial EX.3.4 solution.

RBSE Solutions for Class 10 Maths Chapter 3 Polynomials Ex 3.4.

Class 10 Maths Chapter 3 Polynomials Ex 3.3 Solution is provided in this post. Here we have provide the solutions of RBSE Boards Books according to chapter wise.

Chapter 3 Polynomial EX.3.4 solution.

Rajasthan Board RBSE Class 10 Maths Chapter 3 Polynomials Ex 3.4.

Question 1.
Solve the following equations by the method of completing square.
(i) 3x2 – 5x + 2 = 0
(ii) 5x2 – 6x – 2 = 0
(iii) 4x2 + 3x + 5 = 0
(iv) 4x2 + 4√3x + 3 = 0
(v) 2x2 + x – 4 = 0
(vi) 2x2 + x + 4 = 0
(vii) 4x2 + 4bx – (a2 – b2) = 0
Solution

Question 2.
Find the roots of the following equations (if exists), using Shridhar Acharya quadratic formula.
(i) 2x2 – 2√2x + 1 = 0
(ii) 9x2 + 7x – 2 = 0
(iii) x +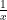  = 3, x ≠ 0
(iv) √2x2 + 7x + 5√2 = 0
(v) x2 + 4x + 5 = 0
(vi)  , x ≠ 0, 2
Solution

Chapter 3 Polynomial EX.3.4 solution.

Question 3.
Find two consecutive odd positive integers, sum of whose square is 290.
Solution
Let x and x + 2 are two consecutive odd positive integers.
According to question,
(x)2 + (x + 2)2 = 290
⇒ x2 + x2 + 4x + 4 = 290
⇒ 2x2 + 4x + 4 = 290
⇒ 2x2 + 4x – 286 = 0
⇒ x2 + 2x – 143 = 0
⇒ x2 + 13x – 11x – 143 = 0
⇒ x(x + 13) – 11(x + 13) = 0
⇒ (x + 13) (x – 11) = 0
⇒ x – 11 = 0
⇒ x = 11
Consecutive odd numbers x = 11
x + 2 = 11 + 2 = 13
Hence, two consecutive odd positve integus are 11, 13

Question 4.
The difference of square of two num¬bers is 45 and square of the smaller number is 4 times the larger number. Find two numbers.
Solution
Let x and y are two number where x > y then
according to question, x2 – y2 = 45 and y2 = 4x
from both equations x2 – 4x = 45
⇒ x2 – 4x – 45 = 0
⇒ x2 – 9x + 5x – 45 = 0
⇒ x(x – 9) + 5 (x – 9) = 0
⇒ (x – 9) (x + 5) = 0
⇒ x – 9 = 0
⇒ x = 9
Larger number (x) = 9
square of smaller number = 4 × 9 = 36
Smaller no. = ±√36 = ±6
Hence, numbers are 9, 6 or 9, -6

Chapter 3 Polynomial EX.3.4 solution.

Question 5.
Divide 16 into two part such that twice the square of larger part is more, then 164 from the square of the smaller part.
Solution
Let larger part be x
Smaller part = 16 – x
According to question,
2x2 = (16 – x)2 + 164
⇒ 2x2 – (16 – x)2 – 164 = 0
⇒ 2x2 – [256 – 32x + x2] – 164 = 0
⇒ 2x2 – 256 + 32x – x2 – 164 = 0
⇒ x2 + 32x – 420 = 0
⇒ x2 + 42x – 10x – 420 = 0
⇒ x(x + 42) – 10(x + 42) = 0
⇒ (x + 42) (x – 10) = 0
⇒ x = -42 or x = 10
⇒ x = 10 [x = -42 not possible]
Larger number (x) = 10
Smaller number (16- x) = 16 – 10 = 6
Hence two numbers are 10, 6

Hope that the Solutions provided here for Class 10 Maths Chapter 3 Polynomials Ex 3.3 will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 3 Polynomials Exercise 3.3 drop a comment below and like and share the post.

Thank you.