Chapter 15 Circumference and Area of a Circle Ex 15.3

RBSE Solutions for Class 10 Maths Chapter 15 Circumference and Area of a Circle

Class 10 Maths Chapter 15 Circumference and Area of a Circle Ex 15.3 Solution is provided in this post. Here we have provide the solutions of RBSE Boards Books according to chapter wise.

Rajasthan Board RBSE Class 10 Maths Chapter 15 Circumference and Area of a Circle Ex 15.3

Question 1.

Find the circumference of circle Inscribed in a square of sides 14 cm.

Solution :

Given

Side of square = 14 cm

Diameter of circle inscribed in square = side of square = 14 cm

Thus, radius of circle is r = 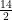 = 7 cm

The circumference of circle = 2πr

=  = 44 cm

Thus circumference of inscribed circle = 44 cm

Question 2.

The difference between radius and circumference of a circle is 74 cm. Find area of this circle.

Solution :

Let r be the radius of circle

According to question

Circumference of circle – radius = 74

Area of circle = πr2

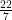=  × (14)2 = 

= 616 sq cm

Question 3.

In given figure 0 is center of circle, ∠AOB = 90° and OA = 3 cm area of shaded part.

Solution :

Given :

In given figure 0 is center of circle and ∠AOB = 90°, radius of circle OA = 3 cm

Area of shaded part

Area of shaded part

= Area of sector OARB – Area of ΔOAB

= 7.07 – 4.5

= 2.57 sq cm

Thus, area of shaded part = 2.57 sq cm

Question 4.

If perimeter of a circle is equal to perimeter of a square, then find ratio of their areas.

Solution :

Let radius of circle r cm

and side of square = a cm

According to question

Perimeter of circle = Perimeter of square

⇒ 2 πr = 4a

⇒  =  = 

Thus, required ratio = 14 : 11

Question 5.

The radius of a circular park is 3.5 m and it is surrounded by 1.4 m broad footpath. Find the area of footpath.

Solution :

Let O is center of circle with center O and radius 3.5 m. Along the outsides of this circle 1.4 m broad path is made.

Thus, r1 = 3.5 m

Radius of park with footpath r2 = 3.5 + 1.4 = 4.9 m

Question 6.

Find the area of square inscribed in a circle of radius 8 cm.

Solution :

Given:

Radius of circle r = 8 cm

So diameter of circle = 2 × r

= 2 × 8 = 16 cm

Square is inside the circle

Diameter of circle and diagonals of square will be same.

Thus, diagonal of square = 16 cm

But diagonal of square side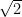 

⇒ side × 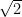 = 16

Question 7.

In given fig. ABMC is a quadrant of a circle of radius 14 cm and a semicircle is drawn assuming BC is diameter. Find the area of shaded region.

Solution :

Radius (r) of quadrant ABMC = 14 cm

∴ Area of shaded part = area of semicircle – [area of quadrant ABMC – area of right angled triangle]

= [154 – (154 – 98)]

= 154 – 154 + 98

= 98 sq cm

Thus, area of shaded part 98 sq. cm

Question 8.

In given figure, AB is diameter of circle AC = 6 cm and BC = 8 cm, then find area of shaded part.

Solution :

Given a circle with center O and AB its diameter

∵ Angle is semicircle is 90°

Thus, ∠ACB = 90°

By Pythagoras theorem

Area of right angled ∆ACB

=  × base × height

=  × 6 × 8

= 24 sq cm

Area of shaded part = Area of circle – area of triangle

= 78.57 – 24 = 54.57 sq cm

Thus area of shaded part = 54.57 sq cm

Question 9.

In given fig., find the area of shaded part where ABCD is a square of side 10 cm and taking each side as diameter, semicircles and drawn. (π = 3.14)

Solution :

Given

Side of square = 10 cm.

in fig. let unshaped part are I, II, III and IV all these part meet at point O in same manner.

= Area of square ABCD – [area of semicircle AOD] + [area of semicircle BOC]

Similarly area of part II + area of part IV

= 21.5 cm2

Thus area of shaded part = area of square ABCD of – area of [I + II + III + IV] part

= (10 × 10) – (21.5 + 21.5)

= 100 – (2 × 21.5)

= 100 – 43 = 57 sq cm

Thus area of shaded part = 57 sq cm

Question 10.

In given figure, radius of semi-circle is 7 cm. Find the area of circle formed in semicircle.

Solution :

Radius of semicircle = 7 cm

Diameter of circle formed in semicircle

= Radius of semicircle = 7 cm

Radius of circle formed is semicircle (r)

=  = 

= 3.5 cm

∴ Area of circle formed in semicircle = πr2

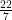=  × (3.5)2

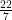=  × (3.5) × (3.5)

= 11 × 3.5 = 38.5 sq cm

Thus area of circle formed in semicircle = 38.5 sq cm

Question 11.

The sum of circumference of two circles of radius R1 and R2 is equal to the circumference of circle of radius R, then correct option is :

(A) R1 + R2 = R

(B)R1 + R2 > R

(C)R1 + R2 < R

(D) nothing is definite

Solution :

Correct option is (A).

Question 12.

The circumference of circle inscribed In a square of side 14cm will be:

(A)22 cm

(B)44 cm

(C) 33 cm

(D) 55 cm

Solution :

Side of square ABCD = 14 cm

Radius of circle inscribed in a square = 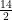 cm

circumference = 2πr

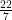=  × 2 × 7 = 44 cm

Thus, option (B) is correct.

We hope that the material provided on this website will be helpful for you. If you have any query regarding any topic related to Rajasthan Board of Secondary education then drop a comment below we will try give you response as soon as possible. if you enjoyed the post,  i'd very grateful if you would help it spread by emailing it to a friend, or sharing it on twitter or facebook. Thank you!