Chapter 10 Area of Triangles and Quadrilaterals Miscellaneous Exercise

Rajasthan Board RBSE Class 9 Maths Solutions Chapter 10 Area of Triangles and Quadrilaterals Miscellaneous Exercise

Multiple Choice Questions

Question 1.
The median of a triangle divides it into two:
(A) triangles of equal area
(B) congruent triangles
(C) right triangles
(D) isosceles triangles
Solution.
(A) triangles of equal area

Question 2.In which of the following figures you find two polygons on the same base and between the same parallels?

Solution.

Question 3.
The figure obtained by joining the mid-points of the adjacent sides of a rectangle of sides 8 cm and 6 cm is:
(A) a rectangle of area 24 cm2
(B) a square of area 25 cm2
(C) a trapezium of area 24 cm2
(D) a rhombus of area 24 cm2
Solution.
(D) a rhombus of area 24 cm2

Question 4.
In figure the area of parallelogram ABCD is:

(A) AB x BM
(B) BC x BN
(C) DC x DL
(D) AD x DL
Solution.
(C) DC x DL

Question 5.
In figure if parallelogram ABCD and rectangle ABEM are of equal area, then:

(A) Perimeter of ABCD = Perimeter of ABEM
(B) Perimeter of ABCD < Perimeter of ABEM (C) Perimeter of ABCD > Perimeter of ABEM
(D) Perimeter of ABCD =  (Perimeter of ABEM)
Solution.
(C) Perimeter of ABCD > Perimeter of ABEM

Question 6.
The mid-points of the sides of a triangle ABC along with any of the vertices as the fourth point make a parallelogram of area equal to:
(A)  ar (∆ABC)
(B)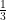  ar (∆ABC)
(C)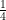  ar (∆ABC)
(D) ar (∆ABC)
Solution.
(A)  ar (∆ABC)

Question 7.
Two parallelograms are on equal bases and between the same parallels. The ratio of their areas is:
(A) 1 : 2
(B) 1 : 1
(C) 2 : 1
(D) 3 : 1
Solution.
(B) 1 : 1

Question 8.
ABCD is a quadrilateral whose diagonal AC divides it into two parts, equal in areas, then ABCD
(A) is always a rectangle
(B) is always a rhombus
(C) is always a parallelogram
(D) None of these
Solution.
(D) None of these

Question 9.
If a triangle and parallelogram are on the same base and between same parallels, then the ratio of the areas of the triangle to the area of the parallelogram is:
(A) 1 : 3
(B) 1 : 2
(C) 3 : 1
(D) 1 : 4
Solution.
(B) 1 : 2

Question 10.
ABCD is a trapezium with parallel sides AB = a cm and DC = b cm (in figure). E and F are the mid-points of the non-parallel sides. The ratio of ar (ABFE) and ar (EFCD) is:

(A) a : b
(B) (3a + b) : (a + 3b)
(C) (a + 3b) : (3a + b)
(D) (2a + b) : (3a + b)
Solution.
(B) (3a + b) : (a + 3b)

Question 11.
In figure, P is any point on median AD of ∆ABC, show that ar (∆ABP) = ar (∆ACP).

Solution.
Here AD is median. Therefore
ar (∆ABD) = ar (∆ACD) …(i)
Reason:
(Median divides the triangle in two parts equal in areas)
Again PD is a median of ∆BPC
ar (∆BPD) = ar (∆CPD) …(ii)
Subtracting (ii) from (i), we get
ar (∆ABD) – ar (∆BPD) = ar (∆ACD) – ar (∆CPD)
⇒ ar (∆ABP) = ar (∆ACP)

Question 12.
In a figure, PQRS and EFRS are two parallelograms then, prove that ar (MFR) =  ar (PQRS).

Solution.
PQRS and EFRS are on the same base SR and between the same parallels EF and SR. So their areas are equal
i.e. ar (PQRS) = ar (EFRS) ….(i)
Also ar (∆MFR) =  ar (EFRS) …(ii)
From equation (i) and (ii), we get
ar (MFR) =  ar (PQRS).
Hence proved.

Question 13.
In the given figure, PSDA is a parallelogram. Point Q and R are taken on PS such PQ = QR = RS and PA || QB || RC. Prove that ar (∆PQE) = ar (∆CFD).

Solution.
Given: PSDA is a parallelogram,
PQ = QR = RS and PQ || QB || RC
To prove: ar (∆PQE) = ar (∆CFD)
Proof: In quadrilateral PABQ,
PQ || AB (∵ PS || AD)
and PA || QB (given)
So, PABQ is parallelogram
PQ = AB …(i)
Similarly, QBCR is also a parallelogram
QR = BC …(ii)
And RCDS is also a parallelogram
RS = CD …(iii)
But PQ = QR = RS (given) …(iv)
From equations (i), (ii), (iii) and (iv), we get
PQ = QR = RS = AB = BC = CD …(v)
Now, in ∆PQE and ∆DCF
∠QPE = ∠FDC (alternate interior angle)
PQ = CD [from equation (v)]
∠PQE = ∠FCD
∠PQE = ∠QBC (alternate interior angles)
and ∠QBC = ∠FCD (corresponding angles)
∆PQE = ∆DCF (by ASA congruencey rule)
Then, ar (∆PQE) = ar (∆DCF) (since, congruent figures have equal area)
Hence proved.

Question 14.
X and Y are points on the side LN of the ALMN such that LX = XY = YN. Through X, a line is drawn parallel to LM to meet MN at Z (see figure). Prove that ar (∆LZY) = ar (quadrilateral MZYX).

Solution.
Given: X and Y are the points on side LN of ∆LMN, such that LX = XY = YN and LM || XZ.
To prove: ar (∆LZY) = ar (quad. MZYX)
Proof: Since ∆XMZ and ∆ZLX are on the same base XZ and between same parallel LM and XZ.
Then, ar (∆XMZ) = ar (∆ZLX) …(i)
On adding ar (∆XYZ) on both sides of equation (i), we get
ar (∆XMZ) + ar (∆XYZ) = ar (∆ZLX) + ar (∆XYZ)
⇒ ar (quad. MZYX) = ar (∆LZY)
Hence proved.

Question 15.
The area of the parallelogram ABCD is 90 cm2. Find
(i) ar (||gm ABEF)
(ii) ar (∆ABD)
(iii) ar (∆BEF)
Solution.
Area of the parallelogram ABCD is 90 cm2

(i) We know that parallelogram on the same base and between the same parallel lines are equal in area
ar (||gm ABEF) = ar (||gm ABCD) = 90 cm2
(ii) We know that, if a triangle and a parallelogram are on the same base and between the same parallels, then area of triangle is equal to half of the area of the parallelogram.
ar (∆ABD) =  ar (||gm ABEF)
(∵ parallelogram lie on same base AB and between same parallels AB and EF)
=  x 90
⇒ ar (∆ABD) = 45 cm2
(iii) Similarly, ABEF and parallelogram ABEF are on the same base EF and EF || AB.
ar (∆BEF) =  ar (||gm ABEF)
=  x 90 = 45 cm2

Question 16.
In the following figure, ABC is a triangle and D is the mid-point of AB. P is any point on BC. Line CQ is drawn parallel to PD to intersect AB at Q. PQ is joined. Show that ar (∆BPQ) =  ar (∆ABC).

Solution.
Given: ∆ABC, in which D is the mid-point of AB.
CQ || PD and CQ intersects AB at Q
To prove: ar (∆BPQ) =  ar (∆ABC)
Construction: Join CD

Proof: Since D is the mid-point of AB. So, on ∆ABC, CD is the median.
Then, ar (∆BCD)=  ar (∆ABC) …(i)
Since, ∆PDQ and ∆PDC are on the same base PD and between same parallels PD and CQ.
Now, ar (∆BCD) =  ar (∆ABC) [using equation (i)]
⇒ ar (∆BDP) + ar (∆PDC) =  ar (∆ABC)
⇒ ar (∆BDP) + ar (∆PDQ) =  ar (∆ABC)
⇒ ar (∆BPQ) =  ar (∆ABC)
Hence proved.

Question 17.
ABCD is a square. E and F are the mid-points of sides BC and CD respectively. If R is the mid-point of line segment EF, then prove that ar (AER) = ar (AFR).
Solution.
ABCD is a square
AB = BC = CD = DA
E and F are mid-points of BC and CD respectively.

In ∆ABE and ∆ADF
AB = AD
BE = DF
∠ABE = ∠ADF = 90°
∆ABE = ∆ADF (by SAS congruency)
⇒ AE = EF (by c.p.c.t)
⇒ ∆AEF is an isosceles triangle,
R is mid-point of EF.
⇒ ∆ARE = ∆ARF. (∵ AE = AF, EF = RF, ∠ARE = ∠ARF = 90°)
⇒ ar (∆AER) = ar (∆AFR)
Hence proved.

Question 18.
O is any point on the diagonal PR of a parallelogram PQRS (in the figure). Prove that ar (∆PSO) = ar (∆PQO).

Solution.
Given: PQRS is a parallelogram and O is any point on the diagonal PR
To prove: ar (∆PSO) = ar (∆PQO)
Construction: Join SQ to intersect PR at B.
Proof: We know that the diagonals of a parallelogram bisect each other, so B is the mid-point of SQ.
Thus PB is a median of ∆QPS and median of a triangle divides it into two triangles of equal area
ar (∆BPQ) = ar (∆BPS) …(i)

Also OB is a median of ∆OSQ
ar (∆OBQ) = ar (∆OBS) …(ii)
On adding equation (i) and (ii), we get
ar (∆BPQ) + ar (∆OBQ) = ar (∆BPS) + ar (∆OSB)
⇒ ar (∆PQO) = ar (∆PSO)
Hence proved.

Question 19.
ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects CD at F. If ar ∆DFB = 3 cm2, then find the area of the parallelogram ABCD.
Solution.
ABCD is a parallelogram and CE = BC i.e. C is the mid-point of BE.

Also, ar (∆DFB) = 3 cm2
We know that ∆DFB and ∆ADF are on the same base DF and between same parallels AB and DF.
Then,
ar (∆ADF) = ar (∆DFB) = 3 cm2 …(i)
Now, in ∆ABE, by converse of mid-point theorem,
EF = AF …(ii) (since C is the mid-point of BE)
In ∆ADF and ∆CFE
∠AFD = ∠CFE (vertically opposite angles)
AF = EF [from equation (ii)]
and ∠DAF = ∠CFE (alternate interior angles)
∆ADF = ∆CFE (by ASA congruence rule)
⇒ ar (∆ADF) = ar (∆CFE) (since congruent figures have equal area)
ar (∆CFE) = ar (∆ADF) = 3 cm2 …(iii) [from equation (i)]
Now, in ∆BFE, C is the mid-point of BE, i.e. CF is the median of ∆BFE
ar (∆CFE) = ar (∆BFC) (since median of a triangle divides it into two triangles of equal areas)
Using equation (iii), we get
ar (∆BFC) = 3 cm2 …(iv)
Now, we have
ar (∆BDC) = ar (∆DFB) + ar (∆BFC) = 3 + 3 = 6 cm2 [using equation (i) and (iv)]
In parallelogram ABCD,
ar (∆ABD) = ar (∆BDC)
(since, diagonal of a parallelogram divides it into two congruent triangles of equal areas)
or, ar (∆BDC) =  ar (||gm ABCD)
(||gm ABCD) = 2 ar (∆ABC) = 2 x 6 = 12 cm2
Hence, the area of parallelogram ABCD is 12 cm2.

Question 20.
A point E is taken on the side BC of parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar (∆ADF) = ar (∆BFC).

Solution.
(ABCD) = ar (ABFC) …(i)
ar (∆ABF) = ar (∆AFC)
ar ∆AFC =  ar (∆BCD) …(ii)
Also ar (∆ADC) =  ar (∆BCD) …(iii)
⇒ ar (∆AFC) = ar (∆ADC) …(iv)
⇒ ar (∆ADF) = ar (∆ADC) + ar (∆ACF) =  ar (∆BCD) +  ar (∆BFC) [using (ii) and (iii)]
=  ar (∆BFC) +  ar (∆BFC)
= ar (∆BFC)
⇒ ar (∆ADF) = ar (∆BFC)
Hence proved.

Question 21.
Diagonals of a parallelogram ABCD bisect at O. A line is drawn through O which meets AD at P and BC at Q. Show that PQ divides ABCD into two parts equal in area.
Solution.
Given: ABCD is a parallelogram in which AC and BD meet at O. A line is drawn through O meets AD at P and BC at Q.

ar (ABQP) = ar (PQCD) =  ar (ABCD)
Proof: AC is a diagonal of parallelogram ABCD
ar (∆ADC) = ar (∆ABC) …(i)
Also ∆OAP = ∆OQC (by ASA congruency property)
[i.e. ∠1 = ∠2, ∠4 = ∠3 and OA = OC]
⇒ ar (∆OAP) = ar (∆OQC) …(ii)
Subtracting (ii) from (i), we get
ar (∆ADC) – ar (∆OAP) = ar (∆ABC) – ar (∆OQC)
⇒ ar (OPDC) = ar (AOQB)
⇒ ar (OPDC) + ar (AOQC) = ar (AOQB) + ar (OAP)
⇒ ar (PQCD) = ar (ABQP)
Hence proved.

Question 22.
The medians BE and CF of a triangle ABC intersect at G. Prove that area of ∆GBC = area of quad. (AFGE).
Solution.
ar (∆AFC) = ar (∆CBF) (As CF is a median)
ar (∆AFC) =  ar (∆ABC) …(i)

and ar (∆BEC)=  ar (∆ABC) …(ii)
From equation (i) and (ii), we get
⇒ ar (∆AFC) = ar (∆BEC)
Subtracting ar (∆GEC) from both side, we get
ar (∆AFC) – ar (∆GEC) = ar (∆BEC) – ar (∆GEC)
ar ∆FGE = ar (∆BGC)

Question 23.
In the following figure, CD || AE and CY || BA. Prove that ar (∆CBX) = ar (∆AXY).

Solution.
Given: CD || AE and CY || BE
To prove: ar (∆CBX) = ar (∆AXY)
Proof: Since, ∆ABC and ∆BAY both lie on the same base AB and between the same parallel AB and CY.
ar (∆ABC) = (∆BAY)
⇒ ar (∆ABX) + ar (∆CBX) = ar (∆ABX) + ar (∆AXY)
⇒ ar (∆CBX) = ar (∆AXY)
[Eliminating ar (∆ABX) from both sides]
Hence proved.

Question 24.
ABCD is a trapezium in which AB || DC, DC = 30 cm and AB = 50 cm. If X and Y are respectively the mid-points of AD and BC, then prove that
ar (DCYX) =  ar (XYBA).
Solution.
Given: ABCD is a trapezium in which AB || DC, DC = 30 cm and AB = 50 cm.
Also, X and Y are respectively the mid-points of AD and BC.

To prove: ar (DCYX) =  ar (XYBA).
Proof: Now, in ∆DCY and ∆PBY
CY = BY (given)
∠C = ∠B (alternate interior angles)
and ∠3 = ∠2 (vertically interior angles)
∆DCY = ∆PBY (by ASA congruence rule)
Then DC = BP (by c.p.c.t)
⇒ DC = PB = 30 cm
AP = BA + BP = 50 + 30 = 80 cm
Now, in ∆ADP, using mid-point theorem
XY =  AP =  x 80 = 40 cm
Let the distance between AB, XY and DC be h cm.
Now, in trapezium DCYX,
ar (trapezium DCYX)

Hence proved.

Question 25.
In ∆ABC, if L and M are the points on AB and AC respectively such that LM || BC, then prove that ar (∆LOB) = ar (∆MOC).
Solution.
Given: In ∆ABC, L and M are two points on AB and AC, such that LM || BC.

To Prove: ar(∆LOB) = ar(∆MOC)
Proof: MB and LC intersect each other at O.
Since, ∆LBC and ∆MBC both lie on the same base BC and between the same parallel lines BC and LM
ar (∆LBC) = ar (∆MBC)
⇒ ar (∆LOB) + ar (∆BOC) = ar(∆MOC) + ar(∆BOC)
⇒ ar (∆LOB) = ar (∆MOC)
[Eliminating ar (∆BOC) from both sides]
Hence proved.

Question 26.
In the following figure, ABCDE is any pentagon, BP is drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar (ABCDE) = ar (∆APQ).

Solution.
Given: ABCDE is a pentagon, BP || AC and EQ || AD.
To prove: ar (ABCDE) = ar (∆APQ)
Proof: We know that triangles on the same base and between the same parallels are equal in areas.
Now, ar (∆ADE) = ar (∆ADQ) …(i)
(Here, ∆ADQ and ∆ADE lie on the same base AD and between the same parallels AD and EQ)
Similarly, ar (∆CAB) = ar (∆CAP) …(ii) (∵ same base is AC and AC || BP)
On adding equations (i) and (ii), we get
ar (∆ADE) + ar (∆CBA) = ar (∆ADQ) + ar (∆CAP)
Adding ar (∆CDA) both sides, we get
ar (∆ADE) + ar (∆CBA) + ar (∆CDA) = ar (∆ADQ) + ar (∆CAP) + ar (∆CDA)
⇒ ar (ABCDE) = ar (∆APQ)
Hence proved.

Question 27.
If medians of a triangles ABC meet at G, then prove that ar (∆AGC) = ar (∆AGB) = ar (∆BGC) =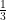  ar (∆ABC)
Solution.
Given: In ∆ABC, medians AD, BE and CF intersect at G.

To prove:
ar (∆AGC) = ar (∆AGB) = ar (∆BGC) =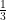  ar (∆ABC)
Proof: We know that median of a triangle divides it into two triangles of equal areas.
In ∆ABC, AD is a median
ar (∆ABD) = ar (∆ACD) …(i)
In ∆CBG, GD is a median
ar (∆GBD) = ar (∆GCD) …(ii)
On subtracting equation (ii) from equation (i), we get
ar (∆ABD) – ar (∆GBD) = ar (∆ACD) – ar (∆GCD)
⇒ ar (∆AGB) = ar (∆AGC)
Similarly,
ar (∆AGB) = ar (∆BGC)
ar (∆AGB) = ar (∆AGC) = ar (∆BGC) …(iii)
But ar (∆ABC) = ar (∆AGB) + ar (∆AGC) + ar (∆BGC) = 3 ar (∆AGB) [from equation (iii)]
ar (∆AGB) =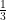  ar (∆ABC)
Hence, ar (∆AGB) = ar (∆AGC) = ar (∆BGC) =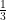  ar (∆ABC)
Hence proved.

Question 28.
In figure, X and Y are the mid-points of AC and AB respectively. QP || BC and CYQ and BXP are straight lines. Prove that ar (ABP) = ar (ACQ).

Solution.
X and Y are mid-point of sides AC and AB respectively.
XY || BC
Clearly, ∆’s BYC and BXC are on the same base BC and lie in between the same parallel lines BC and XY
ar (∆BYC) = ar (∆BXC)
⇒ ar (∆BYC) – ar (∆BOC) = ar (∆BXC) – ar (∆BOC)
⇒ ar (∆BOY) = ar (∆COX)
⇒ ar (∆BOY) + ar (∆XOY) = ar (∆COX) + ar (∆XOY)
⇒ ar (∆BXY) = ar (∆CXY) ….(i)
Similarly quadrilaterals XYAP and XAQY are on the same base XY and between the same parallels XY and PQ
ar (quad. XYAP) = ar (quad. XYQA) …(ii)
Adding corresponding sides of (i) and (ii), we get
ar (∆BXY) + ar (quad. XYAP) = ar (∆CXY) + ar (quad. XYQA)
⇒ ar (∆ABP) = ar (∆ACQ)
Hence proved.

Question 29.
In the given figure, ABCD and AEFD are two parallelograms. Prove that ar (∆PEA) = ar (∆QFD).

Solution.
Given: ABCD and AEFD are two parallelograms.
To prove: ar (∆PEA) = ar (∆QFD)
Proof: In quadrilateral PQDA,
AP || DQ (∵ in parallelogram ABCD, AB || CD)
and PQ || AD (∵ in parallelogram AEFD, FE || AD)
So, PQDA is a parallelogram.
Also, parallelogram PQDA and AEFD are on the same base AD and between same parallels AD and EQ.
ar (||gm PQDA) = ar (||gm AEFD)
On subtracting ar (quadrilateral APFD) from both sides, we get
ar (||gm PQDA) – ar (quadrilateral APFD) = ar (||gm AEFD) – ar (quadrilateral APFD)
⇒ ar (∆QFD) = ar (∆PEA)
Hence proved.