RBSE Solutions for Class 10 Maths Chapter 8 Height and Distance Miscellaneous Exercise
Class 10 Maths Chapter 8 Height and Distance Miscellaneous Exercise Solution is provided in this post. Here we have provide the solutions of RBSE Boards Books according to chapter wise.
RBSE Solutions for Class 10 Maths Chapter 8 Height and Distance Miscellaneous Exercise.
Question 1.
The shadow of a vertical pillar is same the height of pillar, then angle of elevation of sun will be :
(A) 45°
(B) 30°
(C) 60°
(D) 50°
Solution :
Let BC is a tower with height h. Then according to question its shadow AB will be h m.

Let angle of elevation = θ
In right angled ΔABC, we have
tan θ = =
=  = 1
= 1
or tan θ = tan 45°
or θ = tan 45°
Hence, correct choice is (A).
The shadow of a vertical pillar is same the height of pillar, then angle of elevation of sun will be :
(A) 45°
(B) 30°
(C) 60°
(D) 50°
Solution :
Let BC is a tower with height h. Then according to question its shadow AB will be h m.

Let angle of elevation = θ
In right angled ΔABC, we have
tan θ =
or tan θ = tan 45°
or θ = tan 45°
Hence, correct choice is (A).
Question 2.
From a point on the ground which is 100 m away from the foot of the tower, the angle of elevation of the top of the tower is 60°, then height of tower is :
(A) 100 √3 m
(B) m
m
(C) 50 √3 m
(D) m
m
Solution :
Let BC is a tower with height h and angle of elevation is 60° from point A which is 100 m far from tower with base B. So ∠CAB = 60°
In right angled ∆ABC,

tan 60° =
⇒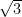 =
= 
So, correct choice is (A)
From a point on the ground which is 100 m away from the foot of the tower, the angle of elevation of the top of the tower is 60°, then height of tower is :
(A) 100 √3 m
(B)
(C) 50 √3 m
(D)
Solution :
Let BC is a tower with height h and angle of elevation is 60° from point A which is 100 m far from tower with base B. So ∠CAB = 60°
In right angled ∆ABC,

tan 60° =
⇒
So, correct choice is (A)
Question 3.
A 15 m long ladder touches the top of a vertical wall. If this ladder makes an angle of 60° with the wall, then height of the wall is : (CBSE 2013)
(A) 15 √3 m
(B) m
m
(C)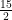 m
m
(D) 15 m
Solution :
Let AB is vertical wall with height h. Let AC is a ladder with length 15 m. Ladder makes an angle 60° from the wall, then ∠ACB = 60°

From right angled ΔABC
cos 60° =
⇒ =
=  ⇒ h =
⇒ h = 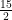 m
m
Hence, correct choice is (C).
A 15 m long ladder touches the top of a vertical wall. If this ladder makes an angle of 60° with the wall, then height of the wall is : (CBSE 2013)
(A) 15 √3 m
(B)
(C)
(D) 15 m
Solution :
Let AB is vertical wall with height h. Let AC is a ladder with length 15 m. Ladder makes an angle 60° from the wall, then ∠ACB = 60°

From right angled ΔABC
cos 60° =
⇒
Hence, correct choice is (C).
Question 4.
From the top of a loom height tower, angle of depression at a point on earth is 30°. Distance of point from base of tower is
(A) 10√3 m
(B) m
m
(C) 10 m
(D) 5√3 m
Solution :
Let BC is a tower with height 10 m. Let the distance of point A from the base of the tower AB = x m and angle of depression is 30° of point A from the top of tower.
Hence, ∠CAB = 30°

From right angled ∆ABC
tan 30° =
⇒ =
=  ⇒ x = 10√3 m
⇒ x = 10√3 m
Hence, correct choice is (A).
From the top of a loom height tower, angle of depression at a point on earth is 30°. Distance of point from base of tower is
(A) 10√3 m
(B)
(C) 10 m
(D) 5√3 m
Solution :
Let BC is a tower with height 10 m. Let the distance of point A from the base of the tower AB = x m and angle of depression is 30° of point A from the top of tower.
Hence, ∠CAB = 30°

From right angled ∆ABC
tan 30° =
⇒
Hence, correct choice is (A).
Question 5.
A bridge above the river makes an angle of 45° with the bank of river. If length of bridge above the river is 150 m, then breadth of river will be :
(A) 75 m
(B) 50√2 m
(C) 150 m
(D) 75√2 m
Solution :
Let AC is a bridge with its length 150 m and BC is a breadth of river. Bridge makes an angle 45° with the river i.e.,
∠CAB = 45°
From right angled ∆ABC
sin 45° =

⇒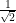 =
= 

Hence, breadth of river 75√2 m
Hence, the correct choice is (D)
A bridge above the river makes an angle of 45° with the bank of river. If length of bridge above the river is 150 m, then breadth of river will be :
(A) 75 m
(B) 50√2 m
(C) 150 m
(D) 75√2 m
Solution :
Let AC is a bridge with its length 150 m and BC is a breadth of river. Bridge makes an angle 45° with the river i.e.,
∠CAB = 45°
From right angled ∆ABC
sin 45° =

⇒

Hence, breadth of river 75√2 m
Hence, the correct choice is (D)
Question 6.
Top of two towers of height 20 m and 14 m are joined by a wire. If wire make an angle of 30° with horizontal line then length of wire is :
(A) 12 m
(B) 10 m
(C) 8 m
(D) 6 m
Solution :
Let two towers are AE and BD where BD = 20 m and AE = 14 m. Let ED is a wire which makes an angle of 30° horizontal line. So

∠DEC = 30°
BD = BC + DC
BD = AE + DC
20 = 14 + DC
DC = 20 – 14 = 6 m
From right angled ∆ECD
sin 30° =
⇒ =
= 
⇒ ED = 6 × 2 = 12 m
Hence, the correct choice is (A).
Top of two towers of height 20 m and 14 m are joined by a wire. If wire make an angle of 30° with horizontal line then length of wire is :
(A) 12 m
(B) 10 m
(C) 8 m
(D) 6 m
Solution :
Let two towers are AE and BD where BD = 20 m and AE = 14 m. Let ED is a wire which makes an angle of 30° horizontal line. So

∠DEC = 30°
BD = BC + DC
BD = AE + DC
20 = 14 + DC
DC = 20 – 14 = 6 m
From right angled ∆ECD
sin 30° =
⇒
⇒ ED = 6 × 2 = 12 m
Hence, the correct choice is (A).
Question 7.
The angle of elevations of the top of the tower from two points distance a and b from the base of tower (a > b) and 30° and 60° then height of tower is :
(A)
(B)
(C)
(D)
Solution :

Let CD is a tower with its height h. Let b is the distance of point B from the base of tower C and a is a distance of point A.
So, ∠CAD = 30°, ∠CBD = 60°
From right angled ∆ACD,
tan 30° =
⇒ =
= 
⇒ h = …..(i)
…..(i)
From right angled ∆BCD,
tan 60° =
⇒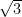 =
=  …(ii)
…(ii)
⇒ h = √3b
From equation (i) and (ii),
h2 = ab
or h =
So, correct choice is (C).
The angle of elevations of the top of the tower from two points distance a and b from the base of tower (a > b) and 30° and 60° then height of tower is :
(A)
(B)
(C)
(D)
Solution :

Let CD is a tower with its height h. Let b is the distance of point B from the base of tower C and a is a distance of point A.
So, ∠CAD = 30°, ∠CBD = 60°
From right angled ∆ACD,
tan 30° =
⇒
⇒ h =
From right angled ∆BCD,
tan 60° =
⇒
⇒ h = √3b
From equation (i) and (ii),
h2 = ab
or h =
So, correct choice is (C).
Question 8.
From the top of a 25 m high pillar at the top of tower angle of elevation is same as the angle of depression of foot of tower then height of tower is :
(A) 25 m
(B) 100 m
(C) 75 m
(D) 50 m
Solution :
Let AE is a pillar in the figure with height 25 m and BD is a tower. According to question at the top of tower angle of elevation is same as the angle of depression of foot of tower.

So ∠CED = ∠CEB = ∠ABE = θ
and AE = BC = 2 m
From right angled ΔBAE
tan θ =
or AB = = 25 cotθ
= 25 cotθ
From right angled ΔECD,
tan θ = =
= 
tan θ =
or CD = 25 cot θ × tan θ
= 25 m [∵ tan θ cot θ = 1]
Hence, height of tower = BC + CD
= 25 + 25
= 50 m
So, correct choice is (D).
From the top of a 25 m high pillar at the top of tower angle of elevation is same as the angle of depression of foot of tower then height of tower is :
(A) 25 m
(B) 100 m
(C) 75 m
(D) 50 m
Solution :
Let AE is a pillar in the figure with height 25 m and BD is a tower. According to question at the top of tower angle of elevation is same as the angle of depression of foot of tower.

So ∠CED = ∠CEB = ∠ABE = θ
and AE = BC = 2 m
From right angled ΔBAE
tan θ =
or AB =
From right angled ΔECD,
tan θ =
tan θ =
or CD = 25 cot θ × tan θ
= 25 m [∵ tan θ cot θ = 1]
Hence, height of tower = BC + CD
= 25 + 25
= 50 m
So, correct choice is (D).
Question 9.
If ratio of length of a vertical rod and length of its shadow is 1 : √3, then angle of elevation of sun is :
(A) 30°
(B) 45°
(C) 60°
(D) 90°
Solution :
Let length of vertical rod is BC and length of shadow is AB.
Let angle of elevation of sun is θ then,

From right ΔABC,
tan θ =
= = tan 30°
= tan 30°
or θ = 30°
Hence, angle of elevation of sun = 30°
So, correct choice is (A).
If ratio of length of a vertical rod and length of its shadow is 1 : √3, then angle of elevation of sun is :
(A) 30°
(B) 45°
(C) 60°
(D) 90°
Solution :
Let length of vertical rod is BC and length of shadow is AB.
Let angle of elevation of sun is θ then,

From right ΔABC,
tan θ =
=
or θ = 30°
Hence, angle of elevation of sun = 30°
So, correct choice is (A).
Question 10.
The slope of a hill makes an angle of 60° with horizontal axis. If to reach at top, 500 m distance have to covered then height of the hill is :
(A) 500√3 m
(B) m
m
(C) 250√3 m
(D) m
m
Solution :
Let height of hill BC = h m
Let slope of hill makes an angle 60° with point A and AC = 500 m and ∠BAC = 60°,

From right angled ∆ABC
sin 60° =
 =
= 
h =
= 250√3
Hence, correct choice is (C).
The slope of a hill makes an angle of 60° with horizontal axis. If to reach at top, 500 m distance have to covered then height of the hill is :
(A) 500√3 m
(B)
(C) 250√3 m
(D)
Solution :
Let height of hill BC = h m
Let slope of hill makes an angle 60° with point A and AC = 500 m and ∠BAC = 60°,

From right angled ∆ABC
sin 60° =
h =
= 250√3
Hence, correct choice is (C).
Question 11.
A tower is vertically placed on a horizontal plane. If angle of elevation of sun is 30 and length of shadow of tower is 45 m, then find height of the tower.
Solution :
Let height of tower is h and length of shadow of tower AB is 45 m. The angle of elevation of sun is 30°.

From right angled ∆ABC
tan 30° =
 =
= 

Hence, height of tower is 15√3 m
A tower is vertically placed on a horizontal plane. If angle of elevation of sun is 30 and length of shadow of tower is 45 m, then find height of the tower.
Solution :
Let height of tower is h and length of shadow of tower AB is 45 m. The angle of elevation of sun is 30°.

From right angled ∆ABC
tan 30° =

Hence, height of tower is 15√3 m
Question 12.
The upper part of a tree is broken by windstorm and it makes an angle of 60° with the ground. The distance from the bottom of the tree to the point where the top touches the ground is 10 m. Find the original height of the tree. (√3 = 1.732)
Solution :
Let length of tree before windstorm is BD.
After windstorm the upper part of tree C falls from point C to point A on the ground.
Now, let CD = AC = h2 m
AB = 10 m
Broken part makes an angle 60° from the ground.

So, ∠CAB = 60°
From right angled ∆ABC
tan 60° =
⇒ √3 =
⇒ h1 = 10√3
and cos 60° =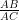
⇒ =
= 
⇒ h2 = 10 × 2
= 20 m
Hence, total length of tree
BD = BC + CD
= h1 + h1
= 10√3 + 20
= 10 × 1.732 + 20
= 17.32 + 20
= 37.32 m
Hence, height of the tree 37.32 m
The upper part of a tree is broken by windstorm and it makes an angle of 60° with the ground. The distance from the bottom of the tree to the point where the top touches the ground is 10 m. Find the original height of the tree. (√3 = 1.732)
Solution :
Let length of tree before windstorm is BD.
After windstorm the upper part of tree C falls from point C to point A on the ground.
Now, let CD = AC = h2 m
AB = 10 m
Broken part makes an angle 60° from the ground.

So, ∠CAB = 60°
From right angled ∆ABC
tan 60° =
⇒ √3 =
⇒ h1 = 10√3
and cos 60° =
⇒
⇒ h2 = 10 × 2
= 20 m
Hence, total length of tree
BD = BC + CD
= h1 + h1
= 10√3 + 20
= 10 × 1.732 + 20
= 17.32 + 20
= 37.32 m
Hence, height of the tree 37.32 m
Question 13.
From a point on the ground which is 120 m away from the foot of the unfinished tower, the angle of elevation of the top of the tower is found to be 30° find how much height of tower have to increased so that its angle of elevation at same point became 60°?
Solution :
Let BC is a incomplete tower with height h1. Point A is 120 m distance from its base B, the angle of elevation is 30° from its top, i.e., ∠BAC = 30°.
Let the tower be given height h2 m till point D. So that angle of elevation becomes 60° from point A.

∠BAD = 60°
From right angled ∆ABC,

From right angled ∆ABD,
tan 60° =
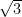 =
= 
h1 + h2 = 120√3
40√3 + h2 = 120√3
h2 = 120√3 – 40√3
= 80√3 m
= 80 × 1.732
CD = 138.56 m
Hence, 138.56 m height of tower have to be increased.
From a point on the ground which is 120 m away from the foot of the unfinished tower, the angle of elevation of the top of the tower is found to be 30° find how much height of tower have to increased so that its angle of elevation at same point became 60°?
Solution :
Let BC is a incomplete tower with height h1. Point A is 120 m distance from its base B, the angle of elevation is 30° from its top, i.e., ∠BAC = 30°.
Let the tower be given height h2 m till point D. So that angle of elevation becomes 60° from point A.

∠BAD = 60°
From right angled ∆ABC,

From right angled ∆ABD,
tan 60° =
h1 + h2 = 120√3
40√3 + h2 = 120√3
h2 = 120√3 – 40√3
= 80√3 m
= 80 × 1.732
CD = 138.56 m
Hence, 138.56 m height of tower have to be increased.
Question 14.
The angle of elevation of the top of a tower from a point situated at 100 m far from the foot of tower is 300. Find the height of the tower.
Solution :
Let height of tower BC = h meter and angle of elevation is 30° from point A which is 100 m from the base B of tower then

∠BAC = 30°
From right angled ∆ABC,

Hence, height of the tower 57.73 m
The angle of elevation of the top of a tower from a point situated at 100 m far from the foot of tower is 300. Find the height of the tower.
Solution :
Let height of tower BC = h meter and angle of elevation is 30° from point A which is 100 m from the base B of tower then

∠BAC = 30°
From right angled ∆ABC,

Hence, height of the tower 57.73 m
Question 15.
The angle of elevation of the top of a pillar from a point on the ground is 15° on walking 100 m towards the tower, the angle of elevation is found to be 30°. Calculate the height of the tower (where tan 15 = 2 – √3).
Solution :
Let CD is a pillar of height h m. The angle of elevation of its top at A be 15°. Let B be a point at a distance of 100 m from A such that the angle of elevation of the top of the tower at B be 30°.
Let BC = x m, so ∠DAC = 15°, ∠DBC = 30°, AB = 100 m

From right angled ∆BCD,
tan 30° =
⇒ =
= 
⇒ x = h√3 m
From right angled ∆ACD,

Hence, height of pillar is 50 m
The angle of elevation of the top of a pillar from a point on the ground is 15° on walking 100 m towards the tower, the angle of elevation is found to be 30°. Calculate the height of the tower (where tan 15 = 2 – √3).
Solution :
Let CD is a pillar of height h m. The angle of elevation of its top at A be 15°. Let B be a point at a distance of 100 m from A such that the angle of elevation of the top of the tower at B be 30°.
Let BC = x m, so ∠DAC = 15°, ∠DBC = 30°, AB = 100 m

From right angled ∆BCD,
tan 30° =
⇒
⇒ x = h√3 m
From right angled ∆ACD,

Hence, height of pillar is 50 m
Question 16.
The shadow of a vertical tower on level ground is increased by 40 m, when the altitude of the sun changes from 60° to 30°. Find the height of the tower.
Solution :
Let CD is a tower of height h. Let from its base C, a point B with distance x, the angle of elevation of top of tower is 60°.
When shadow of tower becomes 40 meter more from B than angle of elevation from A becomes 30°.

Let BC = x m and ∠CBD = 60°, ∠CAD = 30°
From right angled ∆BCD,
tan 60° =
⇒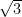 =
= 
⇒ x =
From right angled ∆ACD

Hence, height of tower is 34.64 m
The shadow of a vertical tower on level ground is increased by 40 m, when the altitude of the sun changes from 60° to 30°. Find the height of the tower.
Solution :
Let CD is a tower of height h. Let from its base C, a point B with distance x, the angle of elevation of top of tower is 60°.
When shadow of tower becomes 40 meter more from B than angle of elevation from A becomes 30°.

Let BC = x m and ∠CBD = 60°, ∠CAD = 30°
From right angled ∆BCD,
tan 60° =
⇒
⇒ x =
From right angled ∆ACD

Hence, height of tower is 34.64 m
Question 17.
The angle of depression of two ships from the top of light house situated at 60 m height from sea-level, are 30° and 45° if two ships are on the same side of the light house, then find the distance between two ships.
Solution :
Let AB is a light house of height 60 m and point C and D are two position of ships.

One ship is exactly behind the other on the same side of the light house. The angle of depression of two ships 30° and 45°.
∠PAC = 300 and ∠PAD = 45°
∠ACD = ∠PAC = 30° (alternate angle)
∠ADB = ∠PAD = 45° (alternate angle)
Let CD = x m
From right angled ∆ABD,
tan 45° =
1 =
⇒ BD = 60 m …..(i)
From right angled ∆ABC,

[∵ From equation (i) BD = 60 m]
x + 60 = 60√3
x = 60√3 – 60
= 60(√3 – 1)
= 60 × (1.732 – 1)
= 60 × 0.732
= 43.92 m
Hence, distance between two ships = 43.92 m
The angle of depression of two ships from the top of light house situated at 60 m height from sea-level, are 30° and 45° if two ships are on the same side of the light house, then find the distance between two ships.
Solution :
Let AB is a light house of height 60 m and point C and D are two position of ships.

One ship is exactly behind the other on the same side of the light house. The angle of depression of two ships 30° and 45°.
∠PAC = 300 and ∠PAD = 45°
∠ACD = ∠PAC = 30° (alternate angle)
∠ADB = ∠PAD = 45° (alternate angle)
Let CD = x m
From right angled ∆ABD,
tan 45° =
1 =
⇒ BD = 60 m …..(i)
From right angled ∆ABC,

[∵ From equation (i) BD = 60 m]
x + 60 = 60√3
x = 60√3 – 60
= 60(√3 – 1)
= 60 × (1.732 – 1)
= 60 × 0.732
= 43.92 m
Hence, distance between two ships = 43.92 m
Question 18.
A 1.5 m tall boy is standing at some distance away from a 30 m high building when he moves towards the building then angle of elevation from his eye became 60° from 30°. Find how much distance he covered towards the building?
Solution :
Let PQ be the building of height 30 m. A boy is standing at point R with distance x m from the base of building Q with height QR = 1.5 m, then

OS || PQ and QR || SQ
∴ SQ = OR = 1.5 m
∴ PS = PQ = SQ
= 30 – 1.5 = 28.5 m
The angle of elevation from the eyes of the boy to the top of building is 30° and as the boy walks towards the building the angle of elevation
becomes 60°.
∠PQS = 30° and ∠PTS = 60°
From tight angled ∆PSO,

Let a boy walks some distance and reach point T where the angle of eyes becomes 60° then from right angled ∆PTS,
tan 60° =
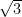 =
= 
TS =
Distance covered toward the building
OT = OS – TS
= 28.5√3 –

Hence, distance walked by the boy towards the building = 19√3 m
A 1.5 m tall boy is standing at some distance away from a 30 m high building when he moves towards the building then angle of elevation from his eye became 60° from 30°. Find how much distance he covered towards the building?
Solution :
Let PQ be the building of height 30 m. A boy is standing at point R with distance x m from the base of building Q with height QR = 1.5 m, then

OS || PQ and QR || SQ
∴ SQ = OR = 1.5 m
∴ PS = PQ = SQ
= 30 – 1.5 = 28.5 m
The angle of elevation from the eyes of the boy to the top of building is 30° and as the boy walks towards the building the angle of elevation
becomes 60°.
∠PQS = 30° and ∠PTS = 60°
From tight angled ∆PSO,

Let a boy walks some distance and reach point T where the angle of eyes becomes 60° then from right angled ∆PTS,
tan 60° =
TS =
Distance covered toward the building
OT = OS – TS
= 28.5√3 –

Hence, distance walked by the boy towards the building = 19√3 m
Question 19.
Angle of elevation of top of a tower from a 7 m high building is 60° and angle of depression of its foot is 45°. Find the height of the tower.
Solution :
Let AB is a tower and CD is a building of height 7 m.
The angle of elevation and angle of depression are 60° and 45° respectively.
i.e., ∠ACE = 60°
and ∠ECB = 45°
BD || CE, CD || BE
∴ CD = BE = 7 m

From right angled ∆CBD
tan 45° =
⇒ 1 =
∴ DB = 7 m
CE = DB = 7 m
Again from right angled ∆AEC
tan 60° =
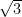 =
= 
AE = 7√ m
Hence, height of tower AB = AE + EB
= 7√3 + 7
= 7(√3 + 1) m
Hence, height of tower AB = 7(√3 + 1) m
Angle of elevation of top of a tower from a 7 m high building is 60° and angle of depression of its foot is 45°. Find the height of the tower.
Solution :
Let AB is a tower and CD is a building of height 7 m.
The angle of elevation and angle of depression are 60° and 45° respectively.
i.e., ∠ACE = 60°
and ∠ECB = 45°
BD || CE, CD || BE
∴ CD = BE = 7 m

From right angled ∆CBD
tan 45° =
⇒ 1 =
∴ DB = 7 m
CE = DB = 7 m
Again from right angled ∆AEC
tan 60° =
AE = 7√ m
Hence, height of tower AB = AE + EB
= 7√3 + 7
= 7(√3 + 1) m
Hence, height of tower AB = 7(√3 + 1) m
Question 20.
From the top of a hill, in east side at two points angle of depressions are 30° and 45°.
If distance between two points is 1 km, then find height of the hill.
Solution :
Let height of hill AB is h km. In the east side of hill there are two points C and D respectively.
The angle of depression are 30° and 45°. The distance between CD = 1 km.

Let AC = x km
From right angled ΔACB
tan 45° =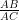
⇒ 1 =
⇒ h = x
From right angled ΔDAB,
tan 30° =
⇒ =
= 
⇒ √3h = x + 1
Put the value of x from equation (i) in equation (ii)
√3h = h + 1
√3h – h = 1
h(√3 – 1) = 1
h = =
=  =
= 
= 1.366 km
Hence, height of hill = 1.366 km
From the top of a hill, in east side at two points angle of depressions are 30° and 45°.
If distance between two points is 1 km, then find height of the hill.
Solution :
Let height of hill AB is h km. In the east side of hill there are two points C and D respectively.
The angle of depression are 30° and 45°. The distance between CD = 1 km.

Let AC = x km
From right angled ΔACB
tan 45° =
⇒ 1 =
⇒ h = x
From right angled ΔDAB,
tan 30° =
⇒
⇒ √3h = x + 1
Put the value of x from equation (i) in equation (ii)
√3h = h + 1
√3h – h = 1
h(√3 – 1) = 1
h =
= 1.366 km
Hence, height of hill = 1.366 km
Question 21.
The angle of elevation of a cloud from a point 20 m above a lake (point A) is 30°. If the angle of depression of its reflection from point A is 60°, then find the distance of cloud from point A.
Solution :
Let BD be the surface of water. A is the point of observation. P be the position of cloud and C be the position of the reflection of cloud in the lake. Draw AQ ⊥ PD. Angle of elevation of cloud from point A is 30° i.e., ∠PAQ = 30° and depression of the reflection of cloud in the lake is 60° i.e, ∠QAC = 60°
Let PQ = h m

So, ∠PAQ = 30° and ∠QAC = 60°
QD = AB = 20 m
CD = PD = (20 + h)m
QC = 20 + h + 20
= (40 + h) m
BD = AQ
From right angled ∆PAQ,
tan 30° =
⇒ =
= 
⇒ AQ = h√3 m
From right angled ∆AQC,
tan 60° =
⇒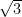 =
=  [∵ From equation (i), AQ = h√3]
[∵ From equation (i), AQ = h√3]
h√3 × √3 = 40 + h
⇒ 3h = 40 + h
⇒ 2h = 40
⇒ h =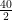 = 20 m
= 20 m
From right angled ∆PAQ
sin 30° =
⇒ =
= 
⇒ =
= 
⇒ AP = 20 × 2 = 40 m
Hence, distance of cloud from A = 40 m
The angle of elevation of a cloud from a point 20 m above a lake (point A) is 30°. If the angle of depression of its reflection from point A is 60°, then find the distance of cloud from point A.
Solution :
Let BD be the surface of water. A is the point of observation. P be the position of cloud and C be the position of the reflection of cloud in the lake. Draw AQ ⊥ PD. Angle of elevation of cloud from point A is 30° i.e., ∠PAQ = 30° and depression of the reflection of cloud in the lake is 60° i.e, ∠QAC = 60°
Let PQ = h m

So, ∠PAQ = 30° and ∠QAC = 60°
QD = AB = 20 m
CD = PD = (20 + h)m
QC = 20 + h + 20
= (40 + h) m
BD = AQ
From right angled ∆PAQ,
tan 30° =
⇒
⇒ AQ = h√3 m
From right angled ∆AQC,
tan 60° =
⇒
h√3 × √3 = 40 + h
⇒ 3h = 40 + h
⇒ 2h = 40
⇒ h =
From right angled ∆PAQ
sin 30° =
⇒
⇒
⇒ AP = 20 × 2 = 40 m
Hence, distance of cloud from A = 40 m
Question 22.
From a point on a bridge across a river, the angles of depression of the banks on opposite side of the river are 30° and 45°, respectively. If the bridge is at height of 4 m from the bank, find the width of the river.
Solution :
Given : Height of bridge from river
AO = 4 m
BO = x, CO = y

From right angled ∆AOB
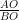 = tan 45°
= tan 45°
⇒ = 1
= 1
⇒ x = 4 m ……(i)
Again from right angled ∆AOC,
 = tan 30°
= tan 30°
⇒ =
= 
⇒ y = 4√3 m ……(ii)
From equation (i) and (ii)
Width of river = x + y
= 4√3 + 4
= 4(√3 + 1)
= 4(1.732 + 1)
= 4(2.732)
= 10.92 m
Hence, width of river is 10.92 m
From a point on a bridge across a river, the angles of depression of the banks on opposite side of the river are 30° and 45°, respectively. If the bridge is at height of 4 m from the bank, find the width of the river.
Solution :
Given : Height of bridge from river
AO = 4 m
BO = x, CO = y

From right angled ∆AOB
⇒
⇒ x = 4 m ……(i)
Again from right angled ∆AOC,
⇒
⇒ y = 4√3 m ……(ii)
From equation (i) and (ii)
Width of river = x + y
= 4√3 + 4
= 4(√3 + 1)
= 4(1.732 + 1)
= 4(2.732)
= 10.92 m
Hence, width of river is 10.92 m
Question 23.
A man on the deck of the ship is 10 m above water-level. He observes that the angle of elevation of the top of hill is 60° and the angle of depression of the base is 30° then find the distance of the hill from the ship and height of the hill.
Solution :
Let AE is a deck of the ship of height 10 m and CD is a hill. From point A, the angle of elevation of the top of hill is 60° and the angle of depression of the base is 30°.
Let BC = h
and ED = x
∠CAB = 60°, ∠BAD = ∠ADE = 30° (Alternate angle)

From right angled ΔAED
tan 30° =
⇒ =
= 
⇒ x = 10√3 m
From right angled ΔABC
tan 60° =
⇒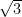 =
= 
⇒ h = 10√3 × √3 = 30 m
Hence, height of hill CD= BD + BC
= 10 + 30 = 40 m
And the distance of the hill from the ship = ED = x = 10√3 m
Hence, distance of the hill from the ship = 10√3 m and height of hill = 40 m.
A man on the deck of the ship is 10 m above water-level. He observes that the angle of elevation of the top of hill is 60° and the angle of depression of the base is 30° then find the distance of the hill from the ship and height of the hill.
Solution :
Let AE is a deck of the ship of height 10 m and CD is a hill. From point A, the angle of elevation of the top of hill is 60° and the angle of depression of the base is 30°.
Let BC = h
and ED = x
∠CAB = 60°, ∠BAD = ∠ADE = 30° (Alternate angle)

From right angled ΔAED
tan 30° =
⇒
⇒ x = 10√3 m
From right angled ΔABC
tan 60° =
⇒
⇒ h = 10√3 × √3 = 30 m
Hence, height of hill CD= BD + BC
= 10 + 30 = 40 m
And the distance of the hill from the ship = ED = x = 10√3 m
Hence, distance of the hill from the ship = 10√3 m and height of hill = 40 m.
Question 24.
A vertical straight tree 12 m high is broken by strong wind in such a way that its top touches the ground and makes an angle of 60° with the ground. Find at what height from the ground did the tree break? (√3 = 1.732)
Solution :
Let BD is a tree of height 12 m. Suppose it got bent at a point C and let the part CD take the position CA, meeting the ground at A.

i.e., CD = AC = h m
(let)
Broken part makes 60° angle from ground So, ∠BAC = 60°
Now height of remaining part of tree = (12 – h)m.
From right angled ∆ABC
sin 60° =
⇒ =
= 
⇒ √3h = 2(12 – h)
⇒ √3h = 24 – 2h
⇒ √3h + 2h = 24
⇒ h(√3 + 2) = 24
⇒ h(1.732 + 2) = 24
⇒ h(3.732) = 24
⇒ h = = 6.4308 m
= 6.4308 m
Hence, height of broken tree from ground = BC
= 12 – h
= 12 – 6.4308
= 5.569 m
Hence, tree ¡s broken 5.569 m from ground.
A vertical straight tree 12 m high is broken by strong wind in such a way that its top touches the ground and makes an angle of 60° with the ground. Find at what height from the ground did the tree break? (√3 = 1.732)
Solution :
Let BD is a tree of height 12 m. Suppose it got bent at a point C and let the part CD take the position CA, meeting the ground at A.

i.e., CD = AC = h m
(let)
Broken part makes 60° angle from ground So, ∠BAC = 60°
Now height of remaining part of tree = (12 – h)m.
From right angled ∆ABC
sin 60° =
⇒
⇒ √3h = 2(12 – h)
⇒ √3h = 24 – 2h
⇒ √3h + 2h = 24
⇒ h(√3 + 2) = 24
⇒ h(1.732 + 2) = 24
⇒ h(3.732) = 24
⇒ h =
Hence, height of broken tree from ground = BC
= 12 – h
= 12 – 6.4308
= 5.569 m
Hence, tree ¡s broken 5.569 m from ground.
Question 25.
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, .which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
Solution :
Let BCD is a highway. A tower is standing at point D of height h. From the top of tower of point A the angle of depression is 30°. After 6 sec when car reaches at point C then angle of depression becomes 60°. Hence distance covered in 6 sec = BC

From right angled ∆ADB,
tan 30° =
⇒ =
= 
⇒ BD = h√3 …..(i)
Again, From right angled ∆ADC,
tan 60° =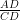
⇒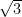 =
= 
⇒ h = √3CD …..(ii)
Put the value of h in equation (i),
BD = √3CD × √3 = 3CD
BC + CD = 3CD
2CD = BC
CD = BC
BC
Since car is moving with uniform speed and distance CD is half of BC.
Hence, time taken to cover distance CD
= × time taken to cover distance BC
× time taken to cover distance BC
= × 6
× 6
= 3 sec.
Hence, required time = 3.
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, .which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
Solution :
Let BCD is a highway. A tower is standing at point D of height h. From the top of tower of point A the angle of depression is 30°. After 6 sec when car reaches at point C then angle of depression becomes 60°. Hence distance covered in 6 sec = BC

From right angled ∆ADB,
tan 30° =
⇒
⇒ BD = h√3 …..(i)
Again, From right angled ∆ADC,
tan 60° =
⇒
⇒ h = √3CD …..(ii)
Put the value of h in equation (i),
BD = √3CD × √3 = 3CD
BC + CD = 3CD
2CD = BC
CD =
Since car is moving with uniform speed and distance CD is half of BC.
Hence, time taken to cover distance CD
=
=
= 3 sec.
Hence, required time = 3.
Question 26.
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower in the same straight line are complementary. Prove that the height of tower is 6 m.
Solution :
Let CD is a tower of height h m. A and B are two points such that AC = 9 m and BC = 4 m.

Let ∠DBC = θ
Then its complement will be ∠DAC = (90° – θ)
From right angled ∆DCB,
tan θ =
tan θ = …..(i)
…..(i)
From right angled ∆DCA,
tan(90° – θ) =
cot θ =
⇒ =
=  …..(i)
…..(i)
multiply equation (i) and (ii),
tan θ × =
=  ×
× 
or 1 =
⇒ h2 = 36
⇒ h = 6 m
Hence, height of tower = 6 m
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower in the same straight line are complementary. Prove that the height of tower is 6 m.
Solution :
Let CD is a tower of height h m. A and B are two points such that AC = 9 m and BC = 4 m.

Let ∠DBC = θ
Then its complement will be ∠DAC = (90° – θ)
From right angled ∆DCB,
tan θ =
tan θ =
From right angled ∆DCA,
tan(90° – θ) =
cot θ =
⇒
multiply equation (i) and (ii),
tan θ ×
or 1 =
⇒ h2 = 36
⇒ h = 6 m
Hence, height of tower = 6 m
Question 27.
A tower and a building on the opposite side of road are situated. The angles depression from the top of tower at the roof and base of building are 45° and 60° respectively. If height of building Is 12 m then find the height of the tower. (√3 = 1.732)
Solution :
Let AB is a building of height 12 m. CE is a tower. Let ED = h m
The angles of depression from point E of top of tower at the roof and base on building are 45° and 60° respectively. Now
∠XEA = ∠EAD = 45° (Alternate angle)
∠XEB = ∠EBC = 60° (Alternate angle)

Let BC = x and ED = h m
AB = CD = 12 m
From right angled ΔEAD,
tan 45° =
l =
⇒ h = x …(i)
From right angled ΔEBC,
tan 60° =
√3 = =
=  (Put the value of x from equation (i))
(Put the value of x from equation (i))
⇒ √3h = h + 12
⇒ √3h – h = 12
⇒ h[1.732 – 1] = 12
⇒ h =
= 16.393 m
Hence, height of tower = EC = CD + ED
= 12 + 16.393
= 28.393 m
A tower and a building on the opposite side of road are situated. The angles depression from the top of tower at the roof and base of building are 45° and 60° respectively. If height of building Is 12 m then find the height of the tower. (√3 = 1.732)
Solution :
Let AB is a building of height 12 m. CE is a tower. Let ED = h m
The angles of depression from point E of top of tower at the roof and base on building are 45° and 60° respectively. Now
∠XEA = ∠EAD = 45° (Alternate angle)
∠XEB = ∠EBC = 60° (Alternate angle)

Let BC = x and ED = h m
AB = CD = 12 m
From right angled ΔEAD,
tan 45° =
l =
⇒ h = x …(i)
From right angled ΔEBC,
tan 60° =
√3 =
⇒ √3h = h + 12
⇒ √3h – h = 12
⇒ h[1.732 – 1] = 12
⇒ h =
= 16.393 m
Hence, height of tower = EC = CD + ED
= 12 + 16.393
= 28.393 m
Question 28.
If angle of elevation of sun changes from 30° to 60°. Then at these angles of elevation find the difference in the length of shadow of 15 m high pillar.
Solution :
Let AD is a pillar of height = 15 m
The angle of elevation from point B of ground is 30° and angle of elevation from point C is 60°.
∠ABD = 30° and ∠ACD = 60°

From right angled ∆ADC

From right angled ∆ADB
tan 30° =
⇒ =
= 
⇒ BD = 15√3 m
Difference in length of shadow = BC
= BD – CD
= 15√3 – 5√3
= 10√3 m
= 10 × 1.732
= 17.32 m
Hence, difference in length of shadow = 17.32 m.
If angle of elevation of sun changes from 30° to 60°. Then at these angles of elevation find the difference in the length of shadow of 15 m high pillar.
Solution :
Let AD is a pillar of height = 15 m
The angle of elevation from point B of ground is 30° and angle of elevation from point C is 60°.
∠ABD = 30° and ∠ACD = 60°

From right angled ∆ADC

From right angled ∆ADB
tan 30° =
⇒
⇒ BD = 15√3 m
Difference in length of shadow = BC
= BD – CD
= 15√3 – 5√3
= 10√3 m
= 10 × 1.732
= 17.32 m
Hence, difference in length of shadow = 17.32 m.
Hope that the Solutions provided here for Class 10 Maths Chapter 8 Height and Distance Miscellaneous Exercise will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 8 Height and Distance Miscellaneous Exercise solution drop a comment below and like and share the post.
Thank you.







0 Comments