Chapter 6 Rectilinear Figures Miscellaneous Exercise

Rajasthan Board RBSE Class 9 Maths Solutions Chapter 6 Rectilinear Figures Miscellaneous Exercise

Multiple Choice Questions (Q1 to Q12)

Question 1.
If two angles of a triangle measures 90° and 30°, the third angle is equal to:
(A) 90°
(B) 30°
(C) 60°
(D) 120°
Answer.
(C) 60°

Question 2.
The three angles of a triangle are in the ratio of 2 : 3 : 4, its greatest angle measures:
(A) 80°
(B) 60°
(C) 40°
(D) 180°
Answer.
(A) 80°

Question 3.
Each angle of an equilateral triangle measures:
(A) 90°
(B) 30°
(C) 45°
(D) 60°
Answer.
(D) 60°

Question 4.
The angles of quadrilateral are in the ratio 1 : 2 : 3: 4, its smallest angle measures.
(A) 120°
(B) 36°
(C) 18°
(D) 10°
Answer.
(C) 18°

Question 5.
In figure, the side BC of a ΔABC has been extended to D. If ∠A = 55° and ∠B = 60° then ∠ACD is:

(A) 120°
(B) 110°
(C) 115°
(D) 125°
Answer.
(C) 115°

Question 6.
The sum of interior angles of a hexagon is:
(A) 720°
(B) 360°
(C) 540°
(D) 1080°
Answer.
(A) 720°

Question 7.
The sum of n exterior angles of an n-sided polygon is:
(A) n right angle
(B) 2n rigjjt angle
(C) (n – 4) right angle
(D) 4 right angle
Answer.
(D) 4 right angle

Question 8.
The number of sides in a regular polygon is n. Then measure of each interior angle is:
(A)  degree
(B) () right angle
(C) n right angle
(D) 2n right angle
Answer.
(B) () right angle

Question 9.
If one angle of a triangle is equal to the sum of the other two angles then the triangle is:
(A) Isosceles triangle
(B) Obtuse angled triangle
(C) Equilateral triangle
(D) Right angled triangle
Answer.
(D) Right angled triangle

Question 10.
One of the exterior angle of a triangle is 105° and its two opposite interior angles are equal, then each of the equal angle is:
(A) 37°
(B) 52°
(C) 72°
(D) 75°
Answer.
(B) 52°

Question 11.
The angles of a triangle are in the ratio 5 : 3 : 7 then the triangle is:
(A) Acute angled triangle
(B) Obtuse angled triangle
(C) Right angled triangle
(D) Isosceles triangle
Answer.
(A) Acute angled triangle

Question 12.
If one of the angle of a triangle is 130° then the angle between the bisectors of the remaining two angles will be
(A) 50°
(B) 65°
(C) 145°
(D) 155°
Answer.
(D) 155°

Question 13.
In figure, find ∠A.

Solution.
∠ACB = 180° – 120° = 60° (due to linear pair)
Exterior ∠B = ∠A + ∠ACB
112° = ∠A + 60°
⇒ ∠A = 52°

Question 14.
In figure, ∠B = 60° and ∠C = 40°. Find the measure of ∠A.

Solution.
∠A + ∠B + ∠C = 180°
⇒ ∠A + 60° + 40° = 180°
⇒ ∠A = 80°

Question 15.
In figure, m || QR then find ∠QPR.

Solution
∠QPR = 180° – (50° + 45°) = 180° – 95° = 85°

Question 16.
In figure, find ∠A.

Solution.
At point B,
100° + ∠ABC = 180° (linear pair angles)
∠ABC = 80°
At point C,
∠DCB + 95° = 180°
⇒ ∠DCB = 85°
Similarly at D,
82° + ∠CDA = 180° (linear pair axiom)
∠CDA = 180° – 82° = 98°
Now in quadrilateral ABCD
∠A + 80° + 85° + 98° = 360° (by angle sum property of a quadrilateral)
⇒ ∠A = 360° – 263°
⇒ ∠A = 97°.

Question 17.
The four angles of a pentagon are 40°, 75°, 125°, and 135° respectively. Find the fifth angle.
Solution.
Suppose fifth angle be x
x + 40° + 75° + 125° + 135° = 540° (sum of interior angles of a pentagon)
⇒ x + 375° = 540°
⇒ x = 540° – 375°
⇒ x = 165°

Question 18.
Each exterior angle of a regular polygon is 45°. Find the number of sides in the polygon.
Solution.
Measure of each exterior angle = 
n =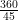  = 8
Hence number of sides in the polygon = 8.

Question 19.
A regular polygon has 12 sides, find the measure of each of its interior angles.
Solution.

Question 20.
The sum of the interior angles of a polygon is 10 right angles. Find the number of sides.
Solution.
Sum of the interior angles of a polygon = 10 right angles = 10 x 90° = 900°
But sum of the interior angles of the polygon = (2n – 4) right angles
i.e. 900 = (2n – 4) x 90°
⇒ 180n – 360 = 900
⇒ 180n = 900 + 360
⇒ 180n = 1260
⇒ n = 7
Hence the required number of sides = 7.

Question 21.
Examine, if it is possible to have a regular polygon whose each interior angle is 110°.
Solution.
Here, it is given that the measure of each interior angle of a regular polygon =110° (if possible)
Hence, measure of each exterior angle = 180° – 110° = 70°.
Suppose number of sides of the polygon = n
But sum of all the n exterior angles = 360°
⇒ n x 70° = 360°
⇒ n = 
= 5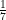 ≠ a whole number.
Hence, a regular polygon having measure of each interior angle 110° can not exist.

Question 22.
In a ∆ABC, ∠A + ∠B = ∠C , then find the greatest angle of the triangle ABC.
Solution.
∠A + ∠B + ∠C = 180° (due to angle sum property)
But ∠A + ∠B = ∠C
⇒ 2∠C = 180°
⇒ ∠C = 90°
Hence greatest angle = 90° which is right angle.

Question 23.
Find the sum of the interior angles of an octagon.
Solution.
The sum of the interior angles of a polygon = (2n – 4) x 90°
Here n = 8
The sum of the interior angles = (2 x 8 – 4) x 90° = (16 – 4) x 90° = 12 x 90° = 1080°

Question 24.
Find the measure of each interior angle of a 10-sided regular polygon.
Solution.

Question 25.
The exterior angles of a triangle obtained by producing, the sides in order are 110°, 130° and x. Find x.
Solution.
The sum of the exterior angles in a polygon = 360°
110° + 130° + x = 360°
⇒ x = 360° – 240°
⇒ x = 120°

Question 26.
One interior angle of a hexagon is 165° and the remaining interior angles are x° each.
Solution.
Sum of the interior angles of a hexagon = 720°
165° + x + x + x + x + x = 720°
⇒ 165° + 5x = 720°
⇒ 5x = 720° – 165° = 555°
⇒ x =  = 111°

Question 27.
In the given figure, if AB || DC then find ∠x, ∠y and ∠z.

Solution.
In ∆BCE
88° = 22° + ∠z (by ext. angle property)
∠z = 88° – 22°
⇒ ∠z = 66°
Also AB || DC
88° + ∠y = 180° (interior angle property)
∠y = 180° – 88°
⇒ ∠y = 92°
Again, 102° + ∠DAB = 180° (linear pair axiom)
∠DAB = 180° – 102° = 78°
AB || DC, then x + 78° = 180° (The sum of the interior angles on the same of a transversal is 180°)
⇒ x = 102°
Hence ∠x = 102°, ∠y = 92°, ∠z = 66°

Question 28.
In figure, if ∠x – ∠y = 10°, then find the measure of ∠x and ∠y.

Solution.
According to figure
∠x + ∠y = 120° …(i) (by exterior angle property)
and ∠x – ∠y = 10° (given) …(ii)
2∠x = 130°
⇒ ∠x = 65°
Now, 65° + ∠y = 120°
⇒ ∠y = 120° – 65°
⇒ ∠y = 55°
Hence, ∠x = 65° and ∠y = 55°.

Question 29.
In a polygon two of its interior angles are each equal to 90° and remaining angles are 150° each. Find the number of sides of the polygon.
Solution.
Suppose number of sides of the polygon be n.
According to problem
2 x 90° + (n – 2) x 150°=(2n – 4) x 90°
⇒ 180 + 150n – 300 = 180n – 360°
⇒ 360 – 300 + 180 = 180n – 150n
⇒ 240 = 30n
⇒ n = 8

Question 30.
From the given figure, prove that ∠x + ∠y = ∠A + ∠C.
Solution.
Construction: Join A to C
In ∆ABC,
∠x = ∠1 + ∠2 …(i) (exterior angle is equal to sum of opposite interior angles)

Also in ∆ADC,
∠y = ∠3 + ∠4 …(ii) (reason as above)
Adding (i) and (ii), we get
∠x + ∠y = ∠1 + ∠2 + ∠3 + ∠4
⇒ ∠x + ∠y = (∠1 + ∠3) + (∠2 + ∠4)
Hence, ∠x + ∠y = ∠A + ∠C
Hence proved.

Question 31.
From figure, find ∠x. Here BO and CO are bisectors of ∠B and ∠C respectively.

Solution.
We know that
∠BOC = 90° +  ∠A
∵ ∠A = 80°
⇒ ∠BOC = 90° +  x 80° = 90° + 40° = 130°

Question 32.
In figure, ∠Q > ∠R and PA is the bisector of ∠QPR and PM ⊥ QR, then prove that ∠APM =  (∠Q – ∠R).

Solution.
Given: In ΔPQR, PA is the bisector of ∠QPR and PM ⊥ QR.
To prove: ∠APM =  (∠Q – ∠R)
Proof: Suppose ∠APR = ∠1, ∠APM = ∠2 and ∠QPM = ∠3
∠1 = ∠2 + ∠3 …(i) [As PA is the bisector of ∠QPR]
In ΔPMR,
∠MPR + ∠PMR + ∠PRM = 180° (angle sum property of a triangle)
⇒ (∠1 + ∠2) + 90° + ∠PRM = 180°
⇒ (∠1 + ∠2) + ∠PRM = 90° …(ii)
Similarly in ΔPQM,
∠3 + ∠Q = 90° …(iii) [As ∠PMQ = 90°]
From (ii) and (iii), we get
∠1 + ∠2 + ∠PRM = ∠3 + ∠Q
⇒ ∠1 + ∠2 + ∠R = ∠3 + ∠Q
⇒ ∠1 + ∠2 – ∠3 = ∠Q – ∠R
⇒ (∠1 – ∠3) + ∠2 = ∠Q – ∠R (as ∠Q > ∠R)
Using relation (i), we get
∠2 + ∠2 = ∠Q – ∠R
⇒ 2∠2 = ∠Q – ∠R
⇒ ∠2 =  (∠Q – ∠R)
⇒ ∠APM =  (∠Q – ∠R)
Hence proved.