Chapter 5 Arithmetic Progression Ex 5.3.

RBSE Solutions for Class 10 Maths Chapter 5 Arithmetic Progression Ex 5.3.

Class 10 Maths Chapter 5 Arithmetic Progression Ex 5.3 solution. Solution is provided in this post. Here we have provide the solutions of RBSE Boards Books according to chapter wise.

Chapter 5 Arithmetic Progression Ex 5.3.

RBSE Solutions for Class 10 Maths Chapter 5 Arithmetic Progression Ex 5.3.

Question 1.
Find the sum of the following A.P.’s
(i) 1, 3, 5, 7, …, upto 12 terms
(ii) 8, 3, -2, …, upto 22 terms
(iii)  upto 11 terms
Solution :
(i) Given A.P. 1, 3, 5, 7 ….. upto 12 terms
First term (a) = 1
Common difference (d) = 3 – 1 ⇒ 2
Sum of n terms
Sn =  [2a + (n – 1)d]
S12 =  [2 × 1 + (12 – 1)2]
= 6[2 + 11 × 2]
= 6[2 + 22]
= 6 × 24
= 144
Hence, sum of first 12 terms = 144.

(ii) Given. A.P. 8, 3, -2, …, upto 22 terms
First term (a) = 8
common difference (d) = 3 – 8 = -5
sum of n terms
Sn =  [2a + (n – 1)d]
=  [2 × 8 + (22 – 1)(-5)]
= 11[16 + 21 × -5]
= 11[16 – 105]
= 11 [- 89]
= -979
Hence, sum of first 22 terms is -979.

(iii) GivenA.P.  upto 11 terms
First term (a) = 
Common difference (d) =  – 
=  =  = 
and number of term n = 11
∵ Sum of n terms Sn =  [2a + (n – 1)d]

Hence, sum of first 11 terms of series = .

Chapter 5 Arithmetic Progression Ex 5.3.

Question 2.
Find the sum of the following :
(i) 3 + 11 + 19 + … 803
(ii) 7 + 10 + 14 + …… + 84
Solution :
(i) Given :
3 + 11 + 19 + … + 803
Here first term a = 3
Common difference d = 11 – 3 = 8
If 803 is nth term of given A.P, then
nth term, an = 803
a + (n – 1)d = 803
3 + (n – 1)8 = 803
(n – 1)8 = 803 – 3
n – 1 = 
n – 1 = 100
n = 100 + 1
n = 101
Hence, A.P. has 101 terms.
∴ Sum of n terms

Thus, 3 + 11+ 15 + … + 803 = 40703.

(ii) Given
7 + 10 + 14 + …. + 84
Here, First term (a) = 7
common difference (d) = 10 – 7 = 3
= 
If 84 is nth term of given series, then
∴ nth term an = 84
a + (n – 1)d = 84
⇒ 7 + (n – 1)  = 84
⇒ 1 +  = 12
⇒  = 12 – 1
⇒  = 11 ⇒ n – 1 = 22
n = 22 + 1 = 23
There are 23 terms in series
Sum of 23 terms

Hence, 7 + 10 + 14 + …… + 84 = 1046.

Chapter 5 Arithmetic Progression Ex 5.3.

Question 3.
Find the number of terms
(i) How many terms of the A.P. : 9, 17, 25 ….. must be taken to give a sum of 636?
(ii) How many terms the A.P. 63, 60, 57, …… must be taken to give a sum of 693?
Solution :
(i) Given A.P. : 9, 17, 25, …
First term (a) = 9, common difference (d) = 17 – 9 = 8
Let no. of terms be n
Sn = 636
⇒  [2a + (n – 1)d] = 636
⇒  [2 × 9+ (n – 1)8] = 636
⇒  [18 + 8n – 8] = 636
⇒  [8n + 10] = 636
⇒ n(4n + 5) = 636
⇒ 4n2 + 5n = 636
⇒ 4n2 + 5n – 636 = 0
⇒ 4n2 + 53 n – 48n – 636 = 0
⇒ n(4n + 53) – 12(4n + 53) = 0
⇒ (4n + 53)(n – 12) = 0
⇒ n – 12 = 0 or 4n + 53 = 0
⇒ n = 12 or – 
∵ n cannot be negative
So, ignore n = – 
∴ n = 12
Hence, sum of 12 terms of given A.P. is 636.

(ii) Given A.P. 63, 60, 57 …..
First term(a) = 63
Common difference (d) = 60 – 63 = -3
Let number of terms be n
Sn = 693
We know that
Sn =  [2a + (n – 1)d]
⇒ 693 =  [2 × 63 + (n – 1) (-3)]
⇒ 693 =  [126 – 3n + 3]
⇒ 1386 = n(129 – 3n)
⇒ 1386 = 129n – 3n2
⇒ 3n2 – 129n + 1386 = 0
⇒ n2 – 43n + 462 = 0
⇒ n2 – 21n – 22n + 462 = 0
⇒ = n(n – 21) – 22(n – 21) = 0
⇒ (n – 21)(n – 22) = 0
⇒ n – 21 = 0 or n – 22 = 0
n = 21 or n = 22
By taking 21 or 22 terms of given A.P. we will get sum 693.

Chapter 5 Arithmetic Progression Ex 5.3.

Question 4.
Find the sum of first 25 terms of following series whose th term is given :
(i) an = 3 + 4n
(ii) an = 7 – 3n
Solution :
(i) Given an = 3 + 4n …..(i)
Substituting various values of n in equation (i)
a1 = 3 + 4(1) = 7
a2 = 3 + 4(2) = 11
a3 = 3 + 4(3) = 15, …
common difference (d) = a2 – a1 = 11 – 7 = 4
a3 – a2 = 15 – 11 = 4
∵ a2 – a1 = a3 – a2 = 4
Thus series is 7, 11, 15 ….
and given series is an A.P.
Here, a = 7, d= 4 and n = 25
∵ Sn =  [2a + (n – 1)d]
S25 =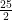  [2 × 7 + (25 – 1)4]
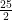=  [14 + 24 × 4]
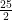=  [14 + 96]
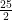=  × 110
= 25 × 55
= 1375
Thus S25 = 1375

(ii)Given : an = 7 – 3n
substituting various values of n in equation (i)
a1 = 7 – 3(1) = 4
a2 = 7 – 3(2) = 1
a3 = 7 – 3(3) = -2
common difference (d) = a2 – a1 = 1 – 4 = -3
and a3 – a2 = -2 – 1 = -3
∵ a2 – a1 = a3 – a2 = -2 – 1 = -3
Thus A.P. is 4, 1, -2,…
Here a = 4 d = -3 and n = 25
We have to find sum of first 25 terms
Sn =  [2a + (n – 1)d]
Sn =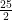  [2 x 4 + (25 – 1)(-3)
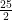=  [8 + 24 × -3]
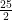=  [8 – 72]
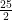=  × – 64
= -25 × 32
= -800
Hence S25 = – 800.

Chapter 5 Arithmetic Progression Ex 5.3.

Question 5.
Find the sum of first 51 terms of AP. in which IInd and IIIrd term are 14 and 18 respectively.
Solution :
Second term of A.P. a2 = 14
and third term a3 = 18
∴ Common difference d = a3 – a2
= 18 – 14 = 4
Again, ∵ IInd term = 14
∴ a + d = 14
⇒ a + 4 = 14
⇒ a = 14 – 4
⇒ a = 10
∵ a = 10, d = 4
Then, sum of n terms Sn =  [2a + (n – 1)d]
∴ S51 =  [2 × 10 + (51 – 1)4]
=  [20 + 50 × 4]
=  [20 + 200]
=  × 220 = 51 × 110 = 5610
Hence, sum of 5 terms of given A.P. = 5610

Question 6.
The first and last term of an A.P. are 17 and 350 respectively. If common difference is 9 then find number of terms in A.P. and their sum.
Solution :
Given
First term (a) = 17
Last term (l) = an = 350
and common difference (d) = 9
∵ an = 350
a + (n – 1)d = 350
⇒ 17 + (n – 1)9 = 350
⇒ 9(n – 1) = 350 – 17 = 333
⇒ n – 1 =  = 37
∴ n = 37 + 1 = 38
Now, Sn = (a + l)
∴ =  (17 + 350)
= 19 × 367 = 6973
Hence, n = 38 and sum of term (Sn) = 6973.

Chapter 5 Arithmetic Progression Ex 5.3.

Question 7.
Find the sum of all odd numbers, divisible by 3 between 1 and 1000.
Solution :
Odd numbers divisible by 3, between 1 and 1000 are 3, 9, 15, 21 …….. 999.
Clearly series 3, 9, 15, 15,21 …… 999 is A.P.
whose first term (a) = 3 and common difference (d) = 6.
Let us assume that this series contains n terms.
∴ an = 999
⇒ a + (n – 1)d = 999
⇒ 3 + (n – 1) × 6 = 999
⇒ 6n – 3 = 999
⇒ 6n = 1002
⇒ n = 
⇒ n = 167
∴ Required sum
Sn =  (a + l)
S167 =  (3 + 999)
=  × 1002
= 167 × 501
= 83667
Hence, required sum = 83667.

Question 8.
The first term of A.P. is 8, nth term is 33 and sum of first n terms is 123, then find n and common difference d.
Solution :
Given
First term (a) = 8
nth term (an) = 33
sum of n terms (Sn) = 123
∵ nth term an = a + (n – 1)d
⇒ 33 = 8 + (n – 1)d
⇒ (n – 1)d = 33 – 8
⇒ (n – 1)d = 25 ……(i)
Now, sum of n terms
Sn =  [2a + (n – 1)d]
⇒ 123 =  [2 × 8 + 25] [From equation (i)]
⇒ 123 =  (16 + 25)
⇒ 123 =  × 41
⇒ n = 
⇒ n = 6
Put the value of n in equation (i)
⇒ (6 – 1)d = 25
⇒ 5d = 25
⇒ d = 5
Thus, n = 6 and d = 5.

Chapter 5 Arithmetic Progression Ex 5.3.

Question 9.
A sum of ₹ 280 is to be used to give four cash prize. If each prize is ₹ 20 less than its preceding prize. Find the value of each of the prizes.
Solution :
Let first prize is ₹ a
∴ IInd prize a2 = ₹ (a – 20)
IIIrd prize a3 = ₹ [(a – 20) – 20]
a3 = ₹ (a – 40)
IVth prize a4 = ₹ [(a – 40) – 20)]
a4 = ₹ (a – 60)
Here first term = a,
Common difference d = (a – 20) – a
d = -20
Number of terms n = 4
Sum of terms Sn = 280
By Formula, Sn =  [2a + (n – 1)d]
S4 =  [2a + (4 – 1) × -20]
⇒ 280 = 2[2a + 3 × – 20]
⇒ 280 = 2[2a – 60]
⇒ 140 = 2a – 60
⇒ 2a = 140 + 60
⇒ a =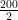  = 100
Hence Ist prize = 100, remaining prize are ₹ (100 – 20), ₹ (100 – 20 – 20) and ₹(100 – 20 – 20 – 20).
Hence price are ₹ 100, ₹ 80, ₹ 60, and 40

Question 10.
A manufacturer of TV sets produced 600 sets in the third year and 700 sets in the seventh year. Assuming that the production increases uniformly by a fixed number every year, find
(i) the production in the Ist year.
(ii) The production in the 10th year.
(iii) The total production in first 7 years.
Solution :
(i) Let production of T.V. sets in first years is a. Given that production of T.V. sets in third year
a3 = 600
and in seventh year
a7 = 100.
Now, a3 = a + (3 – 1)d
600 = a + 2d …..(i)
and a7 = a + (7 – 1)d
700 = a + 6d …(ii)
subtracting eqn (i) from (ii),
100 = 4d
d =  = 25
Put the value of d in equation (i)
⇒ 600 = a + 2 × 25
⇒ 600 = a + 50
⇒ a = 600 – 50
⇒ a = 550
Production of T.V. set in Ist year = 550

(ii) Production of TV. sets in 10th year
Formula, an = a + (n – 1)d
an = 550 + (10 – 1)25
= 550 + 9 × 25
= 550 + 225 = 775
Thus, production of T.V. sets in 10th year = 775 sets
(iii) Total production in 7 years
Sn =  [2a + (n – 1)d]
By formula, S7 =  [2 × 550 + (7 – 1)25]
=  [1100 + 6 × 25]
=  [1100 + 150]
=  × 1250 = 7 × 625
= 4375
Thus, total production in 7 years in 4375 etc.

Chapter 5 Arithmetic Progression Ex 5.3.

Hope that the Solutions provided here for Class 10 Maths Chapter 5 Arithmetic Progression Ex 5.2 will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 5 Arithmetic Progression Ex 5.1 solution drop a comment below and like and share the post.

Thank you.