Chapter 15 Statistics Miscellaneous Exercise

Rajasthan Board RBSE Class 9 Maths Solutions Chapter 15 Statistics Miscellaneous Exercise

Multiple Choice Questions

Question 1.
The frequency of the class interval 3 – 5 in the following distribution is:
5, 5, 6, 4, 9, 5, 3, 2, 7, 6, 3, 8, 4
(A) 3
(B) 4
(C) 6
(D) 7

Question 2.
The range of the following frequency distribution will be:
3.2, 2.8, 3.1, 2.1, 3.2, 2.4, 2.1, 2.8, 2.7, 2.7
(A) 2.7
(B) 3.1
(C) 2.4
(D) 1.1

Question 3.
In the following frequency distribution, the number of students whose age is less than 25 years is:

(A) 8
(B) 16
(C) 9
(D) 25

Question 4.
In a histogram, the heights of the rectangles are:
(A) inversely proportional to the frequencies of their classes.
(B) proportional to the frequencies of the classes.
(C) proportional to the class intervals.
(D) inversely proportional to the class intervals.

Question 5.
The comparative study of the result of any class of a school can be done:
(A) by ogive curve
(B) by histogram
(C) by linear curve
(D) All the above

Question 6.
Range of the distribution 6, 1, 2, 3, 9, 8, 3, 4, 8, 2, 3 is:
(A) 4
(B) 8
(C) 7
(D) 6

Question 7.
If variate of the distribution are 5, 5, 2, 3, 6, 5, 4, then frequency of variate 5 will be:
(A) 1
(B) 2
(C) 3
(D) 4

Question 8.
The median of 11, 2, 7, 8, 9, 3, 5 is:
(A) 7
(B) 9
(C) 5
(D) 10

Question 9.
The mean of 15, 0, 10, 5 will be:
(A) 15
(B) 10
(C) 5
(D) 7.5

Question 10.
The mode of the distribution 4, 3, 4, 5, 4, 2, 4, 1 will be:
(A) 1
(B) 2
(C) 5
(D) 4

Answers
1. B
2. D
3. D
4. B
5. B
6. B
7. C
8. A
9. D
10. D

Very Short Answer Type Questions

Question 11.
Write the frequency of the class interval 0-5 from the distribution 3, 2, 0, 10, 8, 5, 13, 5, 6, 6, 0, 14.
Solution.

Question 12.
If the mean marks of 5, 8, 4, x, 6, 9, is 7, then find the value of x.
Solution.
We have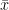  = 7

Question 13.
What is range?
Solution.
The difference of maximum and minimum values of the variate is known as Range.
Range = Maximum value – Minimum value

Question 14.
What is histogram?
Solution.
The rectangular representation of classified and continuous frequency distribution is known as Histogram.

Question 15.
Prepare frequency distribution table from the following data:
9, 7, 9, 8, 3, 9, 8, 3, 5, 7, 5, 3
Solution.

Question 16.
Mean of any frequency distribution is 15 and Σ f = 20, then find the value of Σ fx.
Solution.
We have

Question 17.
Find the median of the following distribution 5, 2, 3, 7, 5, 4, 3, 2, 1.
Solution.
Arranging the given data in ascending order, we get
1, 2, 2, 3, 3, 4, 5, 5, 7
Here, n = 9 (odd)
Median =  th term = 5th term = 3

Question 18.
Find the median of the following distribution 12, 1, 6, 4, 10, 8, 1, 4.
Solution.
Arranging the distribution in ascending order, we get
1, 1, 4, 4, 6, 8, 10, 12
Here, n = 8 (even). So, their will be two median terms
i.e. () th, ( + 1) th
Here,  = 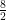 = 4
Median =  =  = 5

Question 19.
Find the mode of the distribution 4, 3, 4, 1, 2, 4, 7, 5, 3.
Solution.
The variate having the maximum frequency, i.e. 3 is 4.
Hence, mode of the distribution is 4.