Chapter 15 Circumference and Area of a Circle Ex 15.1

RBSE Solutions for Class 10 Maths Chapter 15 Circumference and Area of a Circle Ex 15.1

Class 10 Maths Chapter 15 Circumference and Area of a Circle Ex 15.1 Solution is provided in this post. Here we have provide the solutions of RBSE Boards Books according to chapter wise.

Rajasthan Board RBSE Class 10 Maths Chapter 15 Circumference and Area of a Circle Ex 15.1

Question 1.

The radius of a circle is 3.5 cm. Find its area and circumference.

Solution :

Given :

Radius of circle (r) = 3.5 cm

Circumference of circle = 2πr

= 2 × 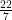 × 3.5

= 22 cm

Area of circle = πr2

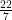=  × (3.5) × (3.5)

= 38.5 cm2

Thus, circumference of circle is 22 cm and area is 38.5 cm2

Question 2.

The circumference of a circle Is 44 m. Find area of circle.

Solution :

Given

Circumference = 44 m

Let radius of circle = r m

Thus, 2πr = 44

⇒ 2 × 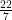 × r = 44

⇒ r = 

= 7 m

Area of circle = πr2

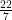=  × 7 × 7

= 154 m2

Thus, area of circle is 154 m2

Question 3.

The radius of a semicircular plot is 21 m. Find its area and perimeter.

Solution :

Given :

Radius of semi-circular plot

(r) = 21 m

Area = πr2

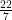=  ×  × 21 × 21

= 693 m2

and perimeter =  × 2πr + 2r

= πr + 2r

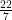=  × 21 + 2 × 21

= 66 + 42

= 108 m

Thus, area of plot ¡s 693 m2 and perimeter is 108 m

Question 4.

The wheel of scooter covered 88 m distance in 100 revolution. Find the radius of wheel

Solution :

Given :

In 100 revolutions, wheel covered a distance of 88 m.

Distance covered by wheel in 1 rotation = circumference of wheel

=  m

=  × 100 cm

= 14 cm

Thus, radius of wheel = 14 cm

Question 5.

The area of a circular plate is 154 cm2. Find its circumference.

Solution :

Given :

Area of circular = 154 cm2

Lei radius of plate i.s r cm, then

πr2 = 154

Circumference of circular plate = 2πr

= 2 × 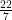 × 7

= 44 cm

Thus, Circumference of circular plate = 44 cm

Question 6.

The circumference of circle is equal to perimeter of a square. If area of square is 484 sq m, then find the area of circle.

Solution:

Let side of square = x m

then perimeter of square 4 × x

and area of square = x2

According to question

Area of square =484 sq m

x2 = 484

x = 

= 22 m

Perimeter of square = 4x = 4 × 22 = 88 m

Let radius of circle is r

circumference of circle = perimeter of square

⇒ 2πr = 88

⇒ 2 × 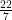 × r = 88

r =  = 14 m

Thus, area of the circle = πr2

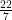=  × 14 × 14 = 616 sq m.

Thus, area of the circle = 616 sq m.

Question 7.

The cost of fencing a circular field at the rate 24 per meter is ₹ 5280 and rate of ploughing is ₹ 0.50 per meter. Find the cost of ploughing the field.

Solution :

Cost of fencing at the rate ₹ 24 per m = ₹ 5280

Let, radius of circular field = r m

Thus, circumference of circular field

Thus, radius of circular field = 35 m

Area of circular field = πr2

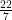=  × 35 × 35 = 3850 sq. m.

∵ cost of ploughing the field 1 m2 = ₹ 0.50

∴ cost of ploughing the field 3850 sq. m.

= 0.50 × 3850 = ₹ 1925

Thus, cost of ploughing the plot = ₹ 1925

Question 8.

The radius of a circular grass field in 35 m. There is 7 m wide ramp around it. Find the area of ramp.

Solution :

Given :

Radius of circular grass field = 35 m.

Width of ramp = 7 m.

R = 35 + 7 = 42 m

Thus area of ramp

Thus, area of ramp is 1694 sq m

Question 9.

The area between two concentric circles will be :

(A) πR2

(B) π (R + r)(R – r)

(C) π(R2 – r)

(D) None of these

Solution :

= πR2 – πr2

= π(R2 – r2)

= π (R + r)(R – r)

Thus, option (B) is correct.

Question 10.

Radius of two concentric circles are 4 cm and 3 cm respectively. Then area bounded by these circles will be:

(A) 22 cm2

(B) 12 cm2

(C) 32 cm2

(D) 18 cm2

Solution :

Given : Radius of two concentre circle are 4 cm and 3 cm.

Thus, R= 4 cm, r = 3 cm

∴ Area between two concentric circles

= π(R2 – r2)

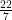=  [(4)2 – (3)2]

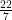=  × [(4 + 3) (4 – 3)]

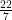=  × 7 = 22 cm2

Thus option (A) is correct.

We hope that the material provided on this website will be helpful for you. If you have any query regarding any topic related to Rajasthan Board of Secondary education then drop a comment below we will try give you response as soon as possible. if you enjoyed the post,  i'd very grateful if you would help it spread by emailing it to a friend, or sharing it on twitter or facebook. Thank you!