Arithmetic Progressions Class 10 Extra Questions

 

Arithmetic Progressions Class 10 Extra Questions Very Short Answer Type

Question 1.
Which of the following can be the nth term of an AP?
4n + 3, 3n2 + 5, n2 + 1 give reason.
Solution:
4n + 3 because nth term of an AP can only be a linear relation in n as an = a + (n – 1)d.

Question 2.
Is 144 a term of the AP: 3, 7, 11, …? Justify your answer.
Solution:
No, because here a = 3 an odd number and d = 4 which is even. so, sum of odd and even must be odd whereas 144 is an even number.

Question 3.
The first term of an AP is p and its common difference is q. Find its 10th term.
Solution:
210 = a + 9d = p + 99.

Question 4.
For what value of k: 2k, k + 10 and 3k + 2 are in AP?
Solution:
Given numbers are in AP
∴ (k + 10) – 2k = (3k + 2) – (k + 10)
⇒ -k + 10 = 2k – 8 or 3k = 18 or k = 6.

Question 5.
If an = 5 – 11n, find the common difference.
Solution:
We have an = 5 – 11n
Let d be the common difference
d = an+1 – an
= 5 – 11(n + 1) – (5 – 11n)
= 5 – 11n – 11 -5 + 11n = -11

Question 6.
If nth term of an AP is 3+n4 find its 8th term.
Solution: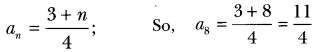

Question 7.
For what value of p are 2p + 1, 13, 5p – 3, three consecutive terms of AP?
Solution:
since 20 + 1, 13, 5p – 3 are in AP.
∴ second term – First term = Third term – second term
⇒ 13 – (2p + 1) = 5p – 3 – 13
⇒ 13 – 2p – 1 = 5p – 16
⇒ 12 – 2p = 5p – 16
⇒ -7p = – 28
⇒ p = 4

Question 8.
In an AP, if d = -4, n = 7, a, = 4 then find a.
Solution:
We know, an = a + (n – 1)d
Putting the values given, we get
⇒ 4 = a + (7 – 1)(-4) or a = 4 + 24
⇒ a = 28

Question 9.
Find the 25th term of the AP: -5, −52 , 0, −52 ………
Solution:
Here, a = -5, b = –52 – (-5) = 52
We know,
a25 = a + (25 – 1 )d
= (-5) + 24(52) = -5 + 60 = 55

Question 10.
Find the common difference of an AP in which a18 – a14 = 32.
Solution:
Given, a18 – a14 = 32
⇒ (a + 17d) – (a + 13d) = 32
⇒ 17d – 13d = 32 or d = 324

Question 11.
If 7 times the 7th term of an AP is equal to 11 times its 11th term, then find its 18th term.
Solution:
Given, 7a7= 11a11
⇒ 7(a + 6d) = 11(a + 100) or 7a + 42d = 11a + 110d
⇒ 4a + 68d = 0 or a + 17d = 0
Now, a18 = a + 17d = 0

Question 12.
In an AP, if a = 1, an = 20, and sn = 399, then find n.
Solution:
Given, An = 20
= 1 + (n – 1)d = 20
⇒ (n – 1) d = 19
sn = n2 {2a + (n – 1)d}
⇒ 399 = n2{2 × 1 + 19}
⇒ 399×221 = n
⇒ n = 38

Question 13.
Find the 9th term from the end (towards the first term) of the AP 5, 9, 13, …, 185.
Solution:
l = 185, d = 4
l9 = l – (n – 1) d
= 185 – 8 × 4 = 153