Chapter 4 Linear Equations in Two Variables Ex 4.2

Rajasthan Board RBSE Class 9 Maths Solutions Chapter 4 Linear Equations in Two Variables Ex 4.2

Solve each of the following systems of simultaneous linear equations by the method of substitution. [Q1. to Q6.]

Question 1.
2x + 3y = 9
3x + 4y = 5
Solution.
The given equations are
2x + 3y = 9 ….(i)
and 3x + 4y = 5 ….(ii)
From (i) 2x = 9 – 3y

Hence, the required solution is x = – 21 and y = 17.

Question 2.
x + 2y = – 1
2x – 3y = 12
Solution
The given equations are
x + 2y = – 1 ..(i)
and 2x – 3y = 12 …(ii)
From (i) x = – 1 – 2y …(iii)
Substituting this value of x in (ii), we get
2( – 1 – 2y) – 3y = 2
⇒ – 2 – 4y – 3y = 12
⇒ – 7y = 14
⇒ y = -2
Putting y = – 2 in (iii), we get
x = -1-2×(-2) = -1+4 = 3
Hence the required solution is x = 3 and y = – 2.

Question 3.
3x + 2y = 11
2x + 3y = 4
Solution
The given equations are
3x + 27 = 11 ….(i)
and 2x + 3y = 4 …(ii)
From (i) 2y = 11 – 3x

Hence the required solution is x = 5 and y = – 2

Question 4.
8x + 5y = 9
3x + 2y = 4
Solution
The given equations are
8x + 5y = 9 …(i)
and 3x + 2y = 4 …(ii)
From (ii) 2y = 4 – 3x

Hence, the required solution is x = – 2 and y = 5.

Question 5.
4x – 5y = 39
2x – 7y = 51
Solution
The given equations are
4x – 5y = 39 …(i)
and 2x – 7y = 51 …(ii)
From equation (ii),
2x – 51 = 7y

Hence the required solution is x = 1, y = -7.

Question 6.
5x – 2y = 19
3x + y = 18
Solution
The given equations are
5x – 2y = 19 …(i)
and 3x + y = 18 …(ii)
From (ii), y = 18 – 3x …(iii)
Substituting y from (iii) in (i), we get
5x – 2(18 – 3x) = 19
⇒ 5x – 36 + 6x = 19
⇒ 11x = 55
⇒ x = 5
Putting x = 5 in (iii), we get
y = 18 – 3 × 5
y = 18 – 15 = 3
Hence the required solution is x = 5 and y = 3.

Solve each of the following systems of simultaneous linear equations by the method of elimination by equating the coefficient.

Question 7.
2x + y = 13
5x – 3y = 16
Solution
The given equations are
2x + y = 13 …(i)
and 5x – 3y= 16 …(ii)
Multiplying equation (i) by 3 and then adding in (ii), we get
11x = 55

Substituting the value of x in (i), we get
2 × 5 + y = 13
⇒ 10 + y = 13
⇒ y = 13 – 10 = 3
Hence the required solution is x = 5, y = 3.

Question 8.
0.4x + 0.3y = 1.7
0.7x – 0.2y = 0.8
Solution
The given equations are
0.4x + 0.3y = 1.7 …(i)
0.7x – 0.2y = 0.8 …(ii)
Multiplying equation (i) by 2 and (ii) by 3 and then adding, we get
2.9x = 5.8
⇒ x = 2
Substituting the value of x in (i), we get
0.4 x 2 + 0.3y = 1.7
⇒ 0.3y = 1.7 – 0.8
⇒ 0.3y = 0.9
⇒ y = 3

Question 9.

Solution
The given equations are

Hence the required solution is x = 14 and y = 9

Question 10.
11x + 15y = – 23
7x – 2y = 20
Solution
The given equations are
11x + 15y = – 23 …(i)
and 7x -2y = 20 …(ii)
Multiplying equation (i) by 2 and (ii) by 15 and then adding, we get
127x = 254
⇒ x = 2
Putting x = 2 in (ii), we get
7 × 2 – 2y = 20
⇒ 14 – 20 = 2y
⇒ 2y = – 6
⇒ y = – 3
Hence the required solution is x = 2 and y = – 3.

Question 11.
3x – 7y + 10 = 0
y – 2x = 3
Solution
The given equations are
3x – 7y + 10 = 0 …(i)
and y – 2x = 3 …(ii)
Multiplying equation (i) by 2 and (ii) by 3 and then adding, we get
– 11y = – 11
⇒ y = 1
Putting y = 1 in (ii), we get
1 – 2x = 3 ⇒ 1 – 3 = 2x
⇒ 2x = -2
⇒ x = -1
Hence the required solution is x = – 1 and y = 1

Question 12.
x + 2y =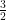 
2x + y =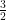 
Solution
The given equations are

Solve each of the following (Q13. to Q15.)

Question 13.
8v – 3u = 5uv
6v – 5u = – 2uv
Solution
The given equations are
8v – 3u = 5uv …(i)
and 6v – 5u = – 2uv …(ii)
Dividing equation (i) and (ii) both side by uv, we get

Question 14.

Solution
The given equations are

Question 15.

Solution
The given equations are

Adding (v) and (vi), we get
2x = 6
⇒ x = 3 and 3 + y = 5
⇒ y = 2
Hence the required solution is x = 3 and y = 2.