chapter 3 Polynomials Ex. 3.1 Solution.

RBSE Solutions for Class 10 Maths Chapter 3 Polynomials Ex 3.1

Class 10 Maths Chapter 3 Polynomials Ex 3.1 Solution s provided in this post. Here we have provide the solutions of Chapter 3 Polynomials Exercise 3.1.

Rajasthan Board RBSE Class 10 Maths Chapter 3 Polynomials Ex 3

Question 1.
Find the zeros of the following quadratic polynomial and test the relation between zeros and coefficients.
(i) 4x2 + 8x
(ii) 4x2 – 4x + 1
(iii) 6x2 – x – 2
(iv) x2 – 15
(v) x2 – (√3 + 1) x + √3
(vi) 3x2 – x – 4
Solution
(i) Given polynomial
f(x) = 4x2 + 8x ⇒ f(x) = 4x(x + 2)
To find zeros of polynomial f(x), f(x) will be zero.
f(x) = 0
⇒ 4x(x + 2) = 0
⇒ x = 0 or x + 2 = 0
⇒ x = 0 or x = -2
Thus zeros of f(x) are 0 and -2
Relations between zeros of polynomial and coefficient.
Sum of zeros = 0 + (-2) = -2
and product of zeros = 0 × -2 = 0

Thus, relation between zeros and polynomial is correct.
(ii) Given polynomial
f(x) = 4x2 – 4x + 1 = (2x)2 – 2 (2x). 1 + (1)2 = (2x – 1)2
To find zeros polynomial f(x), f(x) will be zero.
⇒ (2x – 1)2 = 0
It (2x – 1)2 = 0
⇒ 2x – 1 = 0
⇒ x = 
Here zeros of polynomial are same.
Therefore, zeros of polynomial are  and 
Relation between coefficient and zeros of polynomial

Thus, relation between zeros and polynomial is correct.
(iii) Given polynomial
f(x) = 6x2 – x – 2 = 6x2 – 4x + 3x – 2 = 2x(3x – 2) + 1(3x – 2) = (3x – 2)(2x + 1)
To find zeros of 6x2 – x – 2, f(x) = 0
If 3x – 2 = 0 then 3x = 2 ⇒ x = 
or 2x + 1 = 0 then 2x = -1 ⇒ x =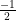 
Therefore zeros of polynomial  , 
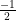
Relation between zeros and coefficient of polynomial

Thus, relation between zeros and polynomial is correct.
(iv) Given polynomial f(x) = x2 – 15
To find zeros of f(x), f(x) will be zero
⇒ f(x) = 0
x2 = 15
or x = ±√15
Therefore zeros of polynomial x2 – 15 are = +√15, -√15
Relation between zeros and coefficient of polynomial
Sum of zeros = √15 – √15 = 0
Product of zeros comparing given polynomial = √15 × (-√15) = -15
Comparing given polynomial x2 – 15 = 0 with ax2 + bx + c
a = 1, b = 0 and c = -15

Thus, relation between zeros and polynomial is correct.
(v) Given polynomial
f(x) = x2 – (√3 + 1) x + √3
= x2 – √3x – x + √3
= x (x – √3) – 1(x – √3)
= (x – √3)(x – 1)
Therefore, f(x) = (x – √3)(x – 1)
To find polynomial f(x), f(x) will be zero.
⇒ f(x) = o
If (x – √3) = 0 then x = √3
or (x – 1) = 0 then x = 1
Therefore, zeros of polynomial are √3, +1
Relation between zeros and coefficient of polynomial
Sum of zeros = (√3 + 1)
product of zeros = √3 × (+1) = √3
comparing given polynomial by ax2 + bx + c
a = 1, b = -(√3 + 1), c = √3

Thus, relation between zeros and polynomial is correct.
(vi) Given polynomial f(x) = 3x2 – x – 4
= 3x2 – (4 – 3) x – 4
= 3x2 – 4x + 3x – 4
= x(3x – 4) + 1(3x – 4)
= (3x – 4) (x + 1)
3x2 – x – 4 = (3x – 4) (x + 1)
To find zeros of f(x),
⇒ f(x) = 0
⇒ (3x – 4)(x + 1) = 0
If 3x – 4 = 0 then 3x = 4 ⇒ x =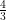 
or x + 1 = 0 then x = -1
Thus, zeros of polynomial are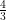  and – 1.
The relation between zeros and coefficient of the polynomial


Thus, relation between zeros and polynomial is correct.

chapter 3 Polynomials Ex. 3.1 Solution.

Question 2.
Find quadratic polynomial. Sum and product of whose zeros are given numbers respectively.
(i) -3, 2
(ii) √2,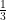 
(iii)  , 
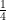
(iv) 0, √5
(v) 4, 1
(vi) 1, 1
Solution
If zeros of quadratic polynomial f(x) are known, then find required polynomial by following formula
Let f(x) = k{x2 – (sum of zeros) x + product of zeros}, where k = a real number
(i) Lef f(x) be a polynomial.
Sum and product of whose zeros are -3 and 2 respectively.
f(x) = k[x2 – (-3)x + 2] = k[x2 + 3x + 2] (∴ k = real number)
Thus required polynomial f(x) = x2 + 3x + 2
(ii) Let f(x) is quadratic polynomial.
Sum and product of whose zeros are √2 and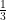  respectively.

where  is a constant term, real number.
Hence, required polynomial is 3x2 – 3√2x + 1
(iii) Let f(x) is a quadratic polynomial sum and product of whose zeros are  and 
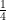
respectively.

Hence, required polynomial is 4x2 + x + 1.
(iv) Let f(x) is a quadratic polynomial.
Sum and product of whose zeros are 0 and √5 respectively.
f(x) = k[ x2 – 0. x + √5 ] = k[x2 + √5 ] (where k is a constant term)
Hence, required polynomial is x2 + √5
(v) Let f(x) is a quadratic polynomial.
Sum and product of whose zeros are 4 and 1 respectively
f(x) = k[x2 – 4x + 1], (where k is constant term)
Hence, required polynomial is x2 – 4x + 1
(vi) Let f(x) is a quadratic polynomial.
Sum and product of whose zeros are 1 and 1 respectively.
f(x) = k{x2 – 1.x + 1) = k(x2 – x + 1), where k is constant term
Hence, required polynomial is x2 – x + 1.

chapter 3 Polynomials Ex. 3.1 Solution.

Question 3.
If sum of square of zeros of quadratic equation f(x) = x2 – 8x + k is 40 then find the value of k.
Solution
Given polynomial f(x) = x2 – 8x + k
Let α and β are zeros of polynomial f(x) then

Now, from equation (i)
(α + β) = 8
Squaring both sides,
(α + β)2 = 82
⇒ a2 + β2 + 2αβ = 64 …(iii)
It is given that sum of square of zeros is 40.
i.e., α2 + β2 = 40
Putting values from equation (i) and (ii) in (iii)
40 + 2k = 64
⇒ 2k = 64 – 40
⇒ 2k = 24
⇒ k = 12
Thus k = 12

Hope that the Solutions provided here for Class 10 Maths Chapter 3 Polynomials Ex 3.1 will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 3 Polynomials Exercise 3.1, drop a comment below and like, share and subscribe the post.

Thank you.