Chapter 17 Measures of Central Tendency Miscellaneous Exercise

Rajasthan Board RBSE Class 10 Maths Chapter 17 Measures of Central Tendency Miscellaneous Exercise

Multiple Choice Questions
Question 1.
Mode of any observation is:
(A) Mid-value
(B) Value having maximum frequency
(C) Minimum frequency value
(D) Range
Solution :
Value having maximum frequency is called mode, so option (B) is correct.

Question 2.
Modal value of the following series is :
520, 20, 340, 190, 35, 800, 1210, 50, 80
(A) 1210
(B) 520
(C) 190
(D) 35
Solution :
Arranging the data is ascending order
20, 35, 50, 80, 190,340, 520, 800, 1210
∵ No. of terms 9 which is odd
∴ Median =  term =  term
=  term = 5th term = 190
Hence, (C) is correct.

Question 3.
53, 75, 42, 70 are marks obtained by 4 students is statistics. Arithmetic mean of their marks is:
(A) 42
(B) 64
(C) 60
(D) 56
Solution :
Given marks = 53, 75, 42, 70

Hence (C) is correct.

Question 4.
A student got 85, 87 and 83 marks in Mathematics, Physics and Chemistry respectively. Mean of obtained marks.
(A) 86
(B) 84
(C) 85
(D) 85.5
Solution :

Thus, (C) is correct.

Question 5.
If 9 is arithmetic mean of 5, 7, 9 and x, then is x :
(A) 11
(B) 15
(C) 18
(D) 16
Solution :
Given 5, 7, 9, x is 9, then

⇒ 36 = 21 + x
⇒ x = 36 – 21 = 15
Thus, (B) is correct.

Question 6.
Median of distribution 2, 3, 4, 7, 5, 1 is:
(A) 4
(B) 7
(C) 11
(D) 3.5
Solution :
Arranging the terms in ascending order 1, 2, 3, 4, 5, 7
Here No. of terms is 6 which is even

=  = 3.5
Thus, (D) is correct.

Question 7.
The median of distribution 1, 3, 2, 5, 9 is:
(A) 3
(B) 4
(C) 2
(D) 20
Solution :
Arranging the terms in ascending order 1, 2, 3, 5, 9
No. of terms is 5 which is odd.
Thus, median =  term =  term
= third term = 3
Thus, (A) is correct.

Question 8.
The mode of distribution 3, 5, 7, 4, 2, 1, 4, 3, 4 is:
(A) 7
(B) 4
(C) 3
(D) 1
Solution:
In the distribution 4 has maximum frequency so mode of distribution = 4
Thus, (B) is correct.

Question 9.
The number of students of a school according to their age are as follows:

Their mode will be:
(A) 41
(B) 12
(C) 3
(D) 17
Solution :
From table it is clear that students of age 12 years have maximum frequency 41.
So mode = 12
Thus, (B) is correct.

Find arithmetic mean of the following distribution (Q. 10 – 14)
Question 10.

Solution :

Arithmetic mean () =  = 7.025
Thus, arithmetic mean = 7.025

Question 11.

Solution :

Arithmetic mean () =  = 21.25
Thus, arithmetic mean = 21.25

Question 12.

Solution :

Arithmetic mean () =  = 25
Thus, arithmetic mean = 25

Question 13.

Solution :

Arithmetic mean () =  = 2
Thus, arithmetic mean = 2

Question 14.
Find arithmetic mean from following frequency distribution.

Solution :
Let A = 50, h = 4

∵ Arithmetic mean () = A +  × h
= 50 +  × 4 = 50 +  = 50 – 0.67 = 50.67
Thus, Required A.M. = 50.67

Find median of following distribution (Q. 15 – 17)
Question 15.

Solution :

Here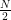  =  = 122.5
Cumulative frequency just above 122.5 is 150 whose corresponding is variable value us 0.4
Thus, median = 0.4

Question 16.

Solution :

Here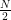  =  = 184.5
Cumulative frequency just above 184.5 is 212 whose corresponding is variable value us 8.0
Thus, required median = 8.0

Question 17.
Runs scored by players of a cricket team are as follows:
57, 17, 26, 91, 115, 26, 83, 41, 57, 0, 26
Find their arithmetic mean, median and mode.
Solution :
(i) For arithmetic mean :

Thus, arithmetic mean = 49 runs

(ii) For median : Arranging the data in ascending order 0, 17, 26, 26, 26, 41, 57, 57, 83, 91, 115
∵ No. of players is 11 which is odd.
⇒ Median =  term
=  term = 6th term = 41
∴ Required median =41

(iii) For mode : Since 26 has maximum frequency so mode = 26.
Thus, arithmetic mean = 49, Median =41 and mode = 26.

Find mode of following distribution : (Q. 18 – 19)
Question 18.

Solution :
Here from table, it is clear that maximum frequency is 13 and its corresponding class is 20 – 40.
So, modal class = 20 – 30
Thus, l = 20, f1 = 13, f0 = 7, f2 = 9 and h = 10

Thus, required mode = 26

Question 19.

Solution :
From table, it is clear that maximum frequency is 24 and its corresponding class is 40 – 60.
Thus, l = 40, f1 = 24, f0 = 15, f2 = 8 and h = 20

Thus, required mode = 26
= 40 + 
= 40 + 7.2 = 47.2
Thus, required mode = 47.2

Question 20.
Write any two demerits of arithmetic mean with its definition.
Solution :
Arithmetic Mean : Arithmetic mean is that value which is obtained by dividing sum of observations by total no. of observations.

Demerits of Arithmetic Mean
(1) Sometimes, by computing mean we get such value which is practically not possible e.g., number of family is 3.8 or 5.6.
(2) In the absence of anyone observation, calculation is not possible.

Question 21.
Write importance of median.
Solution.
Importance of median:
(i) It is only average which is used while dealing with qualitative data.
(ii) It is used for typical value in problems concerning wages, distribution of wealth etc.

Question 22.
Write the formula to find median by grouped frequency distribution:
Solution:

Where l = Lower limit of median
N = Total frequency
C = Cumulative frequency of class preceding the median class
h = Class size
f = Frequency of median class