Rajasthan Board RBSE Class 10 Maths Chapter 16 Surface Area and Volume Ex 16.4
Question 1.
Find the surface area and the volume of a sphere with radius 1.4 cm.
Solution :
Given
Radius of sphere (r) = 1.4 cm
Surface area = 4πr2
= 4 ×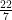 × 1.4 × 1.4
× 1.4 × 1.4
= 24.64 cm2
Volume of the sphere =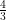 πr2
πr2
=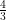 ×
× 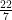 × 1.4 × 1.4 × 1.4
× 1.4 × 1.4 × 1.4
= 11.5 cm3
Hence, surface area of sphere = 24.64 cm2 and its volume = 11.5 cm3
Find the surface area and the volume of a sphere with radius 1.4 cm.
Solution :
Given
Radius of sphere (r) = 1.4 cm
Surface area = 4πr2
= 4 ×
= 24.64 cm2
Volume of the sphere =
=
= 11.5 cm3
Hence, surface area of sphere = 24.64 cm2 and its volume = 11.5 cm3
Question 2.
The surface area of a sphere is 616 cm2. Find the volume of the sphere.
Solution :
Let radius of sphere be r.
Given, Surface area of sphere = 616 cm2
∴ 4πr2 = 616


Hence, volume of sphere = 1437.33 cm3
The surface area of a sphere is 616 cm2. Find the volume of the sphere.
Solution :
Let radius of sphere be r.
Given, Surface area of sphere = 616 cm2
∴ 4πr2 = 616


Hence, volume of sphere = 1437.33 cm3
Question 3.
Radius of a hemisphere is 4.5 cm. Find its total surface area and volume.
Solution :
Given,
Radius of hemisphere (r) = 4.5 cm
Surface area of hemisphere = 3πr2
Let

Hence, total surface area = 190.93 cm2 and volume = 190.93 cm3
Radius of a hemisphere is 4.5 cm. Find its total surface area and volume.
Solution :
Given,
Radius of hemisphere (r) = 4.5 cm
Surface area of hemisphere = 3πr2
Let

Hence, total surface area = 190.93 cm2 and volume = 190.93 cm3
Question 4.
The volume of a sphere is 38808 cm3. Find its surface area.
Solution :
Let radius of the sphere be r,
Volume of sphere = 38808 cm3


Hence, the surface area of sphere = 5544 cm2
The volume of a sphere is 38808 cm3. Find its surface area.
Solution :
Let radius of the sphere be r,
Volume of sphere = 38808 cm3


Hence, the surface area of sphere = 5544 cm2
Question 5.
A cylinder is made of glass, whose radius and height are 4 cm and 10 cm respectively. By melting it, how many sphere with radii 2 cm each can be recasted?
Solution :
Given, for a cylinder
Radius = 4 cm
And height = 10 cm
Volume = πr2h
= π × 4 × 4 × 10 cm3.
Again the radius of a sphere recasted (r) = 2 cm.
Volume of sphere =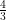 πr2
πr2
=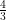 × π × (2)3
× π × (2)3
Let the number of sphere recasted be n, then
Volume of the cylinder = n × volume of sphere

Hence, the number of sphere recasted = 15
A cylinder is made of glass, whose radius and height are 4 cm and 10 cm respectively. By melting it, how many sphere with radii 2 cm each can be recasted?
Solution :
Given, for a cylinder
Radius = 4 cm
And height = 10 cm
Volume = πr2h
= π × 4 × 4 × 10 cm3.
Again the radius of a sphere recasted (r) = 2 cm.
Volume of sphere =
=
Let the number of sphere recasted be n, then
Volume of the cylinder = n × volume of sphere

Hence, the number of sphere recasted = 15
Question 6.
The thickness of hollow spherical shell is 2 cm. If its external radius is 8 cm find the volume of metal used in it.
Solution :
Given,
External radius of hollow spherical shell r1 = 8 cm.
Internal radius r2 = 8 – 2 = 6

Hence, volume of the metal used = 1240.38 cm3
The thickness of hollow spherical shell is 2 cm. If its external radius is 8 cm find the volume of metal used in it.
Solution :
Given,
External radius of hollow spherical shell r1 = 8 cm.
Internal radius r2 = 8 – 2 = 6

Hence, volume of the metal used = 1240.38 cm3
Question 7.
How many cones with radius 3 cm and height 6 cm can be formed by melting a metallic sphere with radius 9 cm.
Solution :
Given,
Radius of sphere (r) = 9 cm
Volume of the sphere =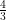 πr3
πr3
=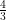 ×
× 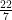 × 9 × 9 × 9 cm3
× 9 × 9 × 9 cm3
For a cone,
Radius (R) = 3 cm
Height (h) = 6 cm
Volume of the cone =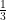 πr2h
πr2h
=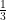 ×
× 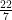 × 3 × 3 × 6 cm3
× 3 × 3 × 6 cm3
Let the number of cones recasted be n.
∴ Volume of sphere = n × volume of a cones

Hence, the number of cones recasted = 54.
How many cones with radius 3 cm and height 6 cm can be formed by melting a metallic sphere with radius 9 cm.
Solution :
Given,
Radius of sphere (r) = 9 cm
Volume of the sphere =
=
For a cone,
Radius (R) = 3 cm
Height (h) = 6 cm
Volume of the cone =
=
Let the number of cones recasted be n.
∴ Volume of sphere = n × volume of a cones

Hence, the number of cones recasted = 54.
Question 8.
Eight spheres of same volumes are recasted by melting a metallic sphere with radius of 10 cm. Find the volume of the recasted sphere.
Solution :
Given,
Radius of the metallic sphere (r) = 10 cm
∴ Volume of sphere =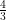 πr3
πr3
=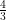 × π × r × (10)3
× π × r × (10)3
Let the radius of each recasted spheres be R.
∴ The volume of large sphere =8 × volume of spheres with radius R

Hence, radius of the sphere casted = 5 cm.
Surface area of sphere = 4πR2
= 4 × π × (5)2
=4 × π × 25
= 100π cm2
Hence, surface area of casted sphere = 100π cm2
Eight spheres of same volumes are recasted by melting a metallic sphere with radius of 10 cm. Find the volume of the recasted sphere.
Solution :
Given,
Radius of the metallic sphere (r) = 10 cm
∴ Volume of sphere =
=
Let the radius of each recasted spheres be R.
∴ The volume of large sphere =8 × volume of spheres with radius R

Hence, radius of the sphere casted = 5 cm.
Surface area of sphere = 4πR2
= 4 × π × (5)2
=4 × π × 25
= 100π cm2
Hence, surface area of casted sphere = 100π cm2
Question 9.
If surface area of a sphere ¡n 5544 cm2, then find its volume.
Solution :
Let radius of sphere be r, then
Given, surface area of sphere = 5544 cm2
4πr2 = 5544

Hence, volume of sphere = 38808 cm3
If surface area of a sphere ¡n 5544 cm2, then find its volume.
Solution :
Let radius of sphere be r, then
Given, surface area of sphere = 5544 cm2
4πr2 = 5544

Hence, volume of sphere = 38808 cm3
Question 10.
The measures of a solid cuboid are 66 cm, 42 cm and 21 cm respectively. How many spheres with diameter 4.2 cm each can be recasted by melting it.
Solution :
Length (l) = 66 cm
Breadth (b) = 42 cm
and height (h) = 21 cm
Volume of cuboid = l × b × h
= 66 × 42 × 21 cm3
Diameter of sphere recasted = 4.2 cm
radius (r) = = 2.1 cm
= 2.1 cm
Volume of sphere =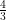 π × (2.1)3
π × (2.1)3
Let by melting the cuboid n spheres are formed.
∴ Volume of cuboid = n × volume of sphere

Hence, the number of sphere reformed = 1500
The measures of a solid cuboid are 66 cm, 42 cm and 21 cm respectively. How many spheres with diameter 4.2 cm each can be recasted by melting it.
Solution :
Length (l) = 66 cm
Breadth (b) = 42 cm
and height (h) = 21 cm
Volume of cuboid = l × b × h
= 66 × 42 × 21 cm3
Diameter of sphere recasted = 4.2 cm
radius (r) =
Volume of sphere =
Let by melting the cuboid n spheres are formed.
∴ Volume of cuboid = n × volume of sphere

Hence, the number of sphere reformed = 1500
Question 11.
A sphere with diameter 6 cm is put into the water filled in a cylindrical vessel with diameter 12 cm. How much the water level in the vessel will rise?
Solution :
Given,
Diameter of sphere = 6 cm
radius (r) =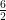 = 3 cm
= 3 cm
Volume of sphere =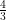 πr3
πr3
=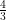 ×
× 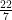 × (3)3
× (3)3
Diameter of cylindrical vessel = 12 cm
radius (R) = = 6 cm
= 6 cm
When the sphere is put into the vessel, the water level rises by h.
∴ Volume of sphere = volume of water rise into cylinder.

Hence, water level will rise in vessel = 1 cm.
A sphere with diameter 6 cm is put into the water filled in a cylindrical vessel with diameter 12 cm. How much the water level in the vessel will rise?
Solution :
Given,
Diameter of sphere = 6 cm
radius (r) =
Volume of sphere =
=
Diameter of cylindrical vessel = 12 cm
radius (R) =
When the sphere is put into the vessel, the water level rises by h.
∴ Volume of sphere = volume of water rise into cylinder.

Hence, water level will rise in vessel = 1 cm.
Question 12.
A hemispherical bowl with internal radius 9 cm is filled with liquid This liquid is to fill into the smaller cylindrical bottle with diameter 3 cm and height 4 cm. How many bottle will be needed to fill whole liquid?
Solution :
Given,
Radius of hemispherical bowl (r) = 9 cm
Volume of the bowl = × π × r3
× π × r3
= × π × (9)3cm3
× π × (9)3cm3
Diameter of cylindrical bottle = 3 cm
Radius =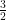 cm
cm
And height = 4 cm
Volume of the bottle = πr2h
= π × 4
× 4
Let n bottles will be needed to be filled the whole Liquid
∴ According to the question.
Volume of hemispherical bowl = n × volume of cylindrical bottles.

Hence, 54 bottles will be needed.
A hemispherical bowl with internal radius 9 cm is filled with liquid This liquid is to fill into the smaller cylindrical bottle with diameter 3 cm and height 4 cm. How many bottle will be needed to fill whole liquid?
Solution :
Given,
Radius of hemispherical bowl (r) = 9 cm
Volume of the bowl =
=
Diameter of cylindrical bottle = 3 cm
Radius =
And height = 4 cm
Volume of the bottle = πr2h
= π
Let n bottles will be needed to be filled the whole Liquid
∴ According to the question.
Volume of hemispherical bowl = n × volume of cylindrical bottles.

Hence, 54 bottles will be needed.
Question 13.
The diameter of a sphere is 0.7 cm. From a water tank, 3000 spheres completely filled with water is thrown out. Find the volume of the
water thrown out.
Solution :
Given,
Diameter of sphere = 0.7 cm
Radius (r) = cm
cm
∴ Volume of sphere V =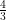 πr3
πr3
=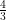 π
π cm3
cm3
Volume of water thrown out = 3000 × volume of sphere
= 3000 ×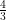 π
π

= 539 cm3
The diameter of a sphere is 0.7 cm. From a water tank, 3000 spheres completely filled with water is thrown out. Find the volume of the
water thrown out.
Solution :
Given,
Diameter of sphere = 0.7 cm
Radius (r) =
∴ Volume of sphere V =
=
Volume of water thrown out = 3000 × volume of sphere
= 3000 ×

= 539 cm3
Question 14.
The external and internal diameters of hemispheric bowl are 43 cm and 42 cm respectively. If the coloring cost is paise 7 per cm2, find the total cost of coloring the bowl.
Solution :
Given,
External diameter of hemispherical bowl = 43 cm
∴ External radius (r1) = cm
cm
Internal diameter = 42 cm
∴ Internal radius (r2) =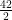 = 21 cm
= 21 cm
External surface area of bowl = 2πr12
And internal surface area = 2πr22

Hence, cost of coloring the bowl = ₹ 397.43
The external and internal diameters of hemispheric bowl are 43 cm and 42 cm respectively. If the coloring cost is paise 7 per cm2, find the total cost of coloring the bowl.
Solution :
Given,
External diameter of hemispherical bowl = 43 cm
∴ External radius (r1) =
Internal diameter = 42 cm
∴ Internal radius (r2) =
External surface area of bowl = 2πr12
And internal surface area = 2πr22

Hence, cost of coloring the bowl = ₹ 397.43






0 Comments