Chapter 12 Surface Area and Volume of Cube and Cuboid Miscellaneous Exercise

Rajasthan Board RBSE Class 9 Maths Solutions Chapter 12 Surface Area and Volume of Cube and Cuboid Miscellaneous Exercise

Multiple Choice Questions

Question 1.
The volume of a cube is 125 cubic metres, its side is:
(A) 7 m
(B) 6 m
(C) 5 m
(D) 2 m
Solution.
(C) 5 m

Question 2.
The volume of a cube is 1331 cubic centimetre, then it surface area is:
(A) 762 sq. cm
(B) 726 sq. cm
(C) 426 sq. cm
(D) 468 sq. cm
Solution.
(B) 726 sq. cm

Question 3.
The length, breadth and height of a cuboid are 4 m, 3 m and 2 m respectively, then surface area of cuboid:
(A) 25 sq. m
(B) 26 sq. m
(C) 52 sq. m
(D) 62 sq. m
Solution.
(C) 52 sq. m

Question 4.
The diagonal of a cuboid having dimension 8mx7mx6mis:
(A) 12.2 m
(B) 12.02 m
(C) 14.2 m
(D) 14.02 m
Solution.
(A) 12.2 m

Question 5.
The edge of a cube is 5 cm, its diagonal
will be:
(A) 4√3cm
(B) 2√3 cm
(C) 5√3 cm
(D) 5 cm
Solution.
(C) 5√3 cm

Question 6.
The volume of cuboid is 400 cubic centimetre, and area of its base is 80 sq. cm, then its height is:
(A) 7 cm
(B) 6 cm
(C) 4 cm
(D) 5 cm
Solution.
(D) 5 cm

Question 7.
A cuboid measuring 15 cm x 12 cm x 6 cm is melted. How many new cubes of sides 3 cm can be made?
Solution.
Required number of new cubes

Question 8.
Two cubical dice having edge 2 cm are joined end to end. Find the total surface area of the solid so formed.
Solution.
Length of the solid = 2 + 2 = 4 cm
Breadth = 2 cm
Height = 2 cm
Surface area = 2(lb + bh + hl)
= 2(4 x 2 + 2 x 2 + 2 x 4)
= 2(8 + 4 + 8)
= 2 x 20
= 40 cm2

Question 9.
An empty tank is 4 m long and 3 m wide. How many cubic metre of water must be filled in .it so that depth of water become 2 m?
Solution.
Length = 4 m, Breadth = 3 m and depth = 2 m
Volume of empty tank = l x b x h = (4 x 3 x 2) m3 = 24 m3
Hence, 24 m3 of water must be filled in the empty tank so that depth of water in the tank becomes 2 m.

Question 10.
A cubical vessel contains 8 litres of water. Find the total surface area of the vessel.
Solution.
Here, volume of vessel = 8 litres
But 1 litre = 1000 cm3
8 litres = 8000 cm3
Let the side of the cubical vessel be l, therefore we can write
Volume = l3
⇒ l3 = 8000
⇒ l3 = (20)3
⇒ l = 20 cm
Now, total surface area is 6l2
Area = 6 x (20)2 = 6 x 400 = 2400
Hence, total surface area = 2400 cm3

Question 11.
A godown measures 60 m x 25 m x 10 m. Find the maximum number of wooden crates each measuring 1.5 m x 1.25 m x 0.5 m that can be stored in the godown.
Solution.
We have,
Length of godown = 60 m
Breadth = 25 m and height = 10 m
Volume/capacity of the godown = (60 x 25 x 10) m3
Volume of one wooden crate = (1.5 x 1.25 x 0.5) m3
Required number of wooden crates

Hence, maximum 16000 crates can be stored in the godown.

Question 12.
A river 3 m deep and 40 m wide is flowing at the rate of 2 km per hour. How much water will fall into the sea in a minute?
Solution.
Water flowed in one minute =  = 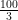 m
Volume of water fell into the sea in one minute
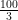=  x 40 x 3 = 4000 m3

Question 13.
The dimension of rectangular parallelopiped are in the ratio 6 : 5 : 4 and its total surface area is 33300 square metres. Find its volume.
Solution.
Let length, breadth and height of a cuboid are 6x, 5x and 4x respectively.
Its total surface area
= 2(lb + bh + hl)
= 2(6x × 5x + 5x × 4x + 4x × 6x)
= 2(30×2 + 20×2 + 24×2)
= 2 x 74×2
= 148×2
But it is given that total surface area = 333000 sq.m
i.e. 148×2 = 33300
⇒ x2 = 
⇒ x2 = 225 m2
⇒ x = √225
⇒ x = 15 m
Dimensions of cuboid are
6x = 6 × 15 = 90 m
5x = 5 × 15 = 75 m
and 4x = 4 × 15 = 60 m
Volume of cuboid = 90 × 75 × 60 cubic metres = 405000 cubic metres.

Question 14.
A field is 20 metres long and 15 metres wide. A pit (outside the field) 10 metres long and 6 metres wide is due to a depth of 5 m and the earth is spread uniformly in the field. By how much the level of field is raised?
Solution.
Dimension of the field are 20 m and 15 m respectively
i.e. length of the field = 20 m
and breadth of the field = 15 m
Now volume of the earth taken out from the pit = l × b × h = 10 × 6 × 5 = 300 cubic metres
Due to 300 cubic metre of earth, suppose the level of field be raised by h metres.
Volume of the field = Volume of earth taken out from the pit
⇒ 20 x 15 x h = 300
⇒ h =  = 1 m
Hence, level of the field be raised by 1 m.