Chapter 12 Circle Ex 12.4

Rajasthan Board RBSE Class 10 Maths Chapter 12 Circle Ex 12.4

Question 1.
An angle of a cyclic quadrilateral is given find its opposite angle.
(i) 70°
(ii) 135°
(iii) 112
(iv)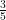  right angle
(v) 165°
Solution :
(i) We know that sum of opposite angles of a cyclic quadrilateral is 180°. Let opposite angle be x°, then
70° + x° = 180°
x° = 180° – 70° = 1 10°
(ii) ∵ Sum of opposite angles of a cyclic quadrilateral is 180°
Let other angle be x°
x° + 135° = 180°
x° = 180°- 13° = 45°
(iii) ∵ Sum of opposite angles of a cyclic quadrilateral is 180°
Let other angle be x°

(iv) Given : first angle =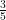  rectangle =  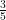× 90° =3 × 18 = 54°
∵ Sum of opposite angles of a cyclic quadrilateral is 180°
Let other angle be x°
x° + 540 = 180°
x° = 180° – 54° = 126°
(v) Let other angle = x°
Sum of opposite angles of a cyclic quadrilateral is 180°
x° + 165° = 180°
x° = 180° – 165° = 15°

Question 2.
Find opposite angle of cyclic quadrilateral if one angle is (i)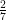  of other
(ii)  of other.
Solution :
(i) Let other opposite angle
So, according to question, first opposite =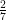 x
We know that sum of opposite angles of cyclic quadrilateral is 180°

Thus, opposite angles of cyclic quadrilateral will be 40°, 140°.
(ii) Let other opposite ∠ = x°
Thus according to question., first opposite ∠ = x ×  = 
We know that sum of opposite angles of cyclic quadrilateral is 180°

Thus, opposite angles of cyclic quadrilateral will be 132°, 48°.

Question 3.
In figure, find all the four angles of cyclic.

Solution :
We know that sum of opposite angles of cyclic quadrilateral is 180°

Question 4.
In figure, some angles are marked a, b, c and d, find them.

Solution :
ABEF and BCDE arc cyclic quadrilateral
∵ We know that sum of opposite angles of cyclic quadrilateral is 180°
Thus, ∠FAB + ∠BEF = 180°
65° + ∠BEF = 180°
∠BEF = 180° – 65° = 115°
and ∠EBA + ∠AFE = 180°
∠EBA + 91° = 180°
∠EBA = 180° – 91° = 89°
We know that exterior angle of cyclic quadrilateral is equal to internal opposite angle
Thus ∠EBC = ∠AFE = 91°
∴ ∠EBC = c = 91°
∠DEB = ∠BAF = 65° = a = 65°
∠EBA = ∠CDE = 89°
∠CDE = b = 89°
∴ ∠BEF = ∠BCD= 115°
∴ ∠BCD = d = 115°
Thus, ∠a = 65°, ∠b = 89°, ∠c = 91°, ∠d = 115°.

Question 5.
If in cyclic quadrilateral ABCD, AD || BC, then Prove that ∠A = ∠D.
Solution :
Given :
ABCD is a cyclic quadrilateral on which AD || BC

To Proved :
∠A = ∠D
Proof : ABCD is a cyclic quadrilateral
We know that sum of opposite angles of a cyclic quadrilateral is 180°
∠A + ∠C = 180°
and ∠B + ∠D = 180° ….(ii)
but ∠A + ∠B = 180° (co-interior corresponding angles) (iii)
From equation (ii) and (iii)
⇒ 2∠A + ∠B + ∠C = ∠B + ∠C + 2∠D
⇒ 2∠A = 2∠D
⇒ ∠A = ∠D

Question 6.
ABCD is a cyclic quadrilateral. produced AB and DC meet at E. Prove that ∆EBNC and ∆EOA arc similar.
Solution :
Given :
ABCD is a cyclic quadrilateral. Produced AB and DC meet at F.

To Prove : ∆EBC ~ ∆EDA
In ∆EBC and ∆EDA
∠EBC = ∠EDA [∵ Exterior of cyclic quadrilateral is equal to interior opposite angle.]
∠ECB = ∠EAD [∵ Exterior of cyclic quadrilateral is equal to interior opposite angle.]
∠E = ∠E (Common angle)
Thus, by AAA similarly
∆EBC ~ ∆EDA

Question 7.
Prove that angle bisectors of cyclic quadrilaterals formed a cyclic quadrilateral.
Solution :
Given :
A cyclic quadrilateral ABCD.
AP, BP, CR and DR are respectively bisector of
∠A, ∠B, ∠C, and ∠D.

To Proved : PQRS is a cyclic quadrilateral.
Proof : To Prove PQRS a cyclic quadrilateral, we should prove
∠APB + ∠CRD = 180°
We know that sum of opposite angles of a cyclic quadrilateral is 180°
Now in ∆APB and ∆CRD


⇒ One pair of opposite angles of quadrilateral PQRS arc supplementary.
⇒ PQRS is a cyclic quadrilateral.