Chapter 11 Area of Plane Figures Miscellaneous Exercise

Rajasthan Board RBSE Class 9 Maths Solutions Chapter 11 Area of Plane Figures Miscellaneous Exercise

Multiple Choice Questions

Question 1.
The length of side of an equilateral triangle is 8 cm, then the area of triangle is:
(A) 16√3 sq.cm
(B) 8√3 sq.cm
(C) 64√3 sq.cm
(D) 4√3 sq.cm
Solution.
(A) 16√3 sq.cm

Question 2.
The sides of a triangle are 40 cm, 70 cm and 90 cm, then the area of triangle is:
(A) 600√5 sq. cm
(B) 500√6 sq. cm
(C) 482√5 sq. cm
(D) 60√5 sq. cm
Solution.
(A) 600√5 sq. cm

Question 3.
The equal sides of an isosceles triangle is 6 cm and another side is 8 cm then its area will be:
(A) 8√5 sq. cm
(B) 5√8 sq. cm
(C) 3√55 sq. cm
(D) 3√8 sq. cm
Solution.
(A) 8√5 sq. cm

Question 4.
The perimeter of an equilateral triangle is 60 cm then its area will be:
(A) 400√3 sq.cm
(B) 100√3 sq.cm
(C) 50√3 sq. cm
(D) 200√3 sq. cm
Solution.
(B) 100√3 sq.cm

Question 5.
The area of a right angled triangle is 36 sq. cm and its base 9 cm then the length of perpendicular will be:
(A) 8 cm
(B) 4 cm
(C) 16 cm
(D) 32 cm
Solution.
(A) 8 cm

Question 6.
The side of any square is 10 cm then its perimeter is:
(A) 20 cm
(B) 10 cm
(C) 40 cm
(D) 30 cm
Solution.
(C) 40 cm

Question 7.
The diagonals of a rhombus are 8 cm and 6 cm then its area will be:
(A) 48 sq. cm
(B) 24 sq. cm
(C) 12 sq. cm
(D) 96 sq. cm
Solution.
(B) 24 sq. cm

Question 8.
If the perimeter of a room is 40 m and its height is 4 m then area of four walls is equal to:
(A) 40 sq. cm
(B) 80 sq. cm
(C) 120 sq, cm
(D) 160 sq. cm
Solution.
(D) 160 sq. cm

Question 9.
Find the length of the side of an equilateral triangle whose area is 9√3 sq. cm.
Solution.
Area of an equilateral triangle =  (side)2
⇒ 9√3 =  (side)2
⇒ 36 = (side)2
⇒ side = 6 cm

Question 10.
Write the formula to find the area of the cyclic quadrilateral.
Solution.
Area of cyclic quadrilateral = 

Question 11.
If the area of a square is 144 Are, then write its perimeter.
Solution.
Area of square =144 Are
⇒ (side)2 = 144 x 100 m2 (∵ 1 Are = 100 m2)
⇒ (side)2 = 14400 m2
⇒ side = 120 m
Perimeter = 4 x one side = 4 x 120 m = 480 m

Question 12.
If the area and base of a parallelogram are 174.60 sq. m and 18 m respectively, write its height.
Solution.
Area of a parallelogram = base x height
base =  =  = 9.7 m

Question 13.
Write the area of the quadrilateral in which length of the diagonal is 6 m and the sum of perpendiculars upon the diagonals is 12 cm.
Solution.
Area of a quadrilateral =  (sum of offsets) x diagonal
=  x 12 x 6 = 36 cm2

Question 14.
Sides of a triangle are in the ratio 25 : 17 : 12 and its perimeter is 540 m. Find its area.
Solution.
Let sides of the triangle be 25x, 17x and 12x.
According to question, perimeter = 540 m
i.e. 25x + 17x + 12x = 540 m
54x = 540 m
⇒ x = 10 m
Sides are 250 m, 170 m, 120 m
⇒ Semi-perimeter (s) =  = 270 m
Area of triangle

Hence, the area of triangle = 9000 m2.

Question 15.
Find the base of an isosceles triangle whose area is 12 sq. cm and length of one of the equal side is 5 cm.
Solution.
Let equal sides be (a) = 5 cm and base (b) = ?
Area of an isosceles triangle = 12 sq. cm
Area of an isosceles triangle

Question 16.
The perimeter of a triangle is 40 cm and two of its sides are 8 cm and 15 cm. Find the area of the triangle and length of the perpendicular of the largest side from the opposite vertex.
Solution.
Perimeter of ∆ABC = 40 cm (given)
i.e., AB + BC + CA = 40 cm
or, 8 + 15 + CA = 40 cm
or, CA = 40 – 23
or, CA = 17 cm

Hence, area of ∆ABC = 60 cm2 and length of the perpendicular on the largest side from the opposite vertex is 7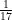 cm.

Question 17.
The perimeter of a rhombus is 146 cm and length of one of its diagonal is 55 cm. Find the other diagonal and area of the rhombus.
Solution.
Perimeter of a rhombus = 146 cm
i.e., 4 x one side = 146

Question 18.
A rhombus shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, how much area of grass field will each cow be getting?
Solution.
Here triangles ABC and ADC are congruent
ar (∆ABC) = ar (∆ADC)

Also triangles ABC and ADC have equal perimeters.

Therefore, area of rhombus ABCD = 2 x area of ∆ABC = 2 x 432 = 864 m2
Also area of grass field each cow will graze =  m2 = 48 m2.

Question 19.
An umbrella is made by stitching 10 triangular pieces of cloth of two different. colours (see figure), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?

Solution.
Here, we are given that sides of one triangular piece of cloth are of length 20 cm, 50 cm and 50 cm respectively.
Semi-perimeter of the triangular piece
s = 
⇒ s = 60

Area of cloth of each colour required for the umbrella = 10 x 200√6 cm2 = 2000√6 cm2.

Question 20.
A trapezium with its parallel sides in the ratio 16 : 5, is cut from a rectangle whose sides are 63 metre and 5 metre respectively. The area of the trapezium is  of the rectangle. Find the length of the parallel sides of the trapezium.
Solution.
Let ABCD be a trapezium with its parallel sides AB and CD.

Here it is given that AB : CD = 16 : 5
i.e., AB and CD = 16x and 5x
We are given that Area of trapezium =  of area of rectangle


Hence, parallel sides are 25.6 m and 8 m respectively.

Question 21.
A rectangular field is of length 99 metre and area 4356 sq. m. A road 4.5 m wide has been constructed centrally in the field parallel to its length and breadth. Find the total number of square blocks of side 1.5 m to cover the road.
Solution.

Area of the rectangular field = 4356 m2
Length of the field = 99 m
Breadth =  =  = 44 m
Width of the road = 4.5 m
Area of the road parallel to the length = 99 x 4.5 = 445.5 m2
Area of the road parallel to the breadth = 44 x 4.5 = 198 m2
and area of the common square portion = 4.5 x 4.5 = 20.25 m2
Total area of the road = 445.50 + 198 – 20.25 = 623.25 sq. m
Area of each square stone = 1.5 x 1.5 sq. m
Required number of stone for the road =  = 277

Question 22.
A room is 8 m 50 cm long and 6 m 50 cm wide. What should be the length of the mat of width 25 cm to cover the whole floor? Find the total cost of the mat at the rate of ₹ 20 per m.
Solution.
Length of room = 8.50 m
Breadth of room = 6.50 m
Area of room = l x b = (8.50 x 6.50) m2
Let length of the mat be x.

Cost of 1 m of mat is ₹ 20
Cost of 221 m of mat = 221 x 20 = ₹ 4, 420.